最近扱われるデータ量は膨大です。それに伴いデータの見方を変え、かつては重要度が低かった点からも関係性を見出す必要があります。
そのために確率推論は多くの命題の生起する可能性を確率として記述することから始められ、条件付き確率と結合確率を1つずつ繋ぎ合わせ段階的に構成されています。

ベイジアンネットワーク(Bayesian network)

人工知能(AI)における確率推論の一つのモデルです。
イギリスの確率論研究家トーマス・ベイズが発案したベイズの定理に基づき、因果関係を確率により記述するグラフィカルモデルの1つであり、「原因」と「結果」の関係を複数組み合わせることにより、「原因」「結果」がお互いに影響を及ぼしながら発生する現象をネットワーク図と確率で可視化したものです。これは「原因」から発生する「結果」を、確率をもって予測する推論手法とも表せます。

ベイジアンネットワークの特徴

• 単純な二方向の計算ではないこと
• 確率(乗算)で表現できること
• 視覚的に操作できること
• チューニングが容易であること
• 人間の意志決定のプロセスと非常に似ていること
• AIでは扱いにくい凡例の少ない事象もベイジアンネットワークでは扱える
• 予測において説明変数の入力に欠損があってもよい
  欠損値に適切な確率分布が割り当てられ、必ずしも予測時に全ての観測値を揃える必要はない。
  
• モデルの利用用途が限定されない
  ベイジアンネットワークは矢印の順方向だけでなく、逆方向にも推論が行える。観測を入力する変数と予測対象となる変数がモデルで限定されることなく自由に選択できる。
  

逆方向の推論？

鍵となるのは、条件付き確率と結合確率の定義です。

結合確率とは事象A、事象Bが同時に起こる確率で、条件付き確率とはどちらかの事象が先に起きた上で他の事象が起こる確率です。
では、以下がそれぞれの定義と逆方向への推論が可能であるかを示したものです。

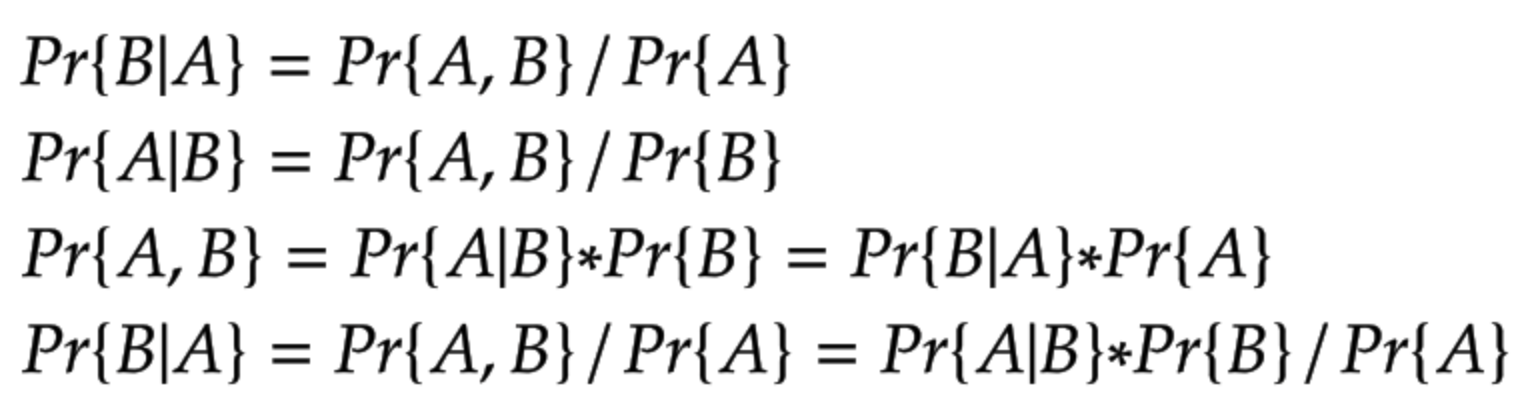
Aが先に起こる確率がわからない場合もBが先に起こる条件付き確率がわかれば推論できます。

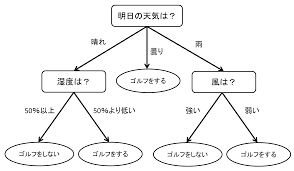
利用シーン

ベイジアンネットワークは様々な事象間の因果関係(厳密には確率的な依存関係)をグラフ構造で表現するモデリング手法の一つで、故障診断、気象予測、医療的意思決定支援、マーケティング、推薦システムなど様々な分野で利用されています。また消費者行動のモデル構築にも応用されています。
今後、ベイジアンネットワークは個人の特徴（行動、性格など）の因果関係を確率として数値化することで、個人の行動パターンや特徴を組み合わせて考えることで新たな可能性を見いだせるはずです。

Twitter・Facebookで定期的に情報発信しています！
Follow @acceluniverse