DEVELOPER’s BLOG
技術ブログ
自然言語処理( NLP )とは -統計的手法を用いて-
2019.11.28
久保 大亮
統計学
自然言語処理

※本記事の対象:自然言語処理という言葉は聞いたことはあるが、どういうアプローチで処理がされているかイメージが湧かない方(大学レベルの数学の知識は必要)
※内容はオーム社『ゼロから学ぶDeep Learning2』を参考にしている
1. はじめに:自然言語処理(NLP)とは
2. シソーラスによる手法
3. カウントベースの手法( 統計的手法 )
4. カウントベースの手法の改善点
5. 【次回】word2vec( ←これがメイン )
6. まとめ
7. 参考文献
そこで 自然言語処理 (Natural Language Processing: NLP )とは、一言で言うと「我々が普段用いてる言葉をコンピュータに理解させるための技術」である。
NLPの目標とするところは、人間が話す「同じような文章でも意味や表現が異なるような」言葉をコンピュータに理解させ、我々にとって有益なことをコンピュータに行わせることである。例えば機械翻訳、検索エンジン、文章の感情分析などが挙げられる。
我々の身の回りではそのような自然言語処理の技術がすでに数多く使われている。
我々の使う言葉は「文字」によって構成され、言葉の意味は「単語」によって構成されている。「単語」は、言わば意味の最小単位である。
つまるところ、自然言語をコンピュータに理解させるには、「単語の意味」を理解させることが重要であるといえそうだ。
そこで本記事では「単語の意味」をうまく捉えた表現方法について「シソーラス」による手法、「カウントベース」の手法の2つを見ていく。
しかし自然言語の歴史を振り返ると、『広辞苑』のように人が使う一般的な辞書ではなく 、 シソーラス (thesaurus)と呼ばれるタイプの辞書が多く使われてきた。
シソーラスとは「類語辞書」のことで、「同義語」や「類義語」が同じグループに分類されている。例えば、「car」という単語に対して、
 のようにいくつかの同義語が存在することが分かる。
のようにいくつかの同義語が存在することが分かる。
また、自然言語処理において利用されるシソーラスでは、単語間で「上位と下位(is a の関係)」、「全体と部分(part-of の関係)」などのより細かい関係性が定義されている場合がある。次のようなグラフ構造によって各単語の関係性が定義される。
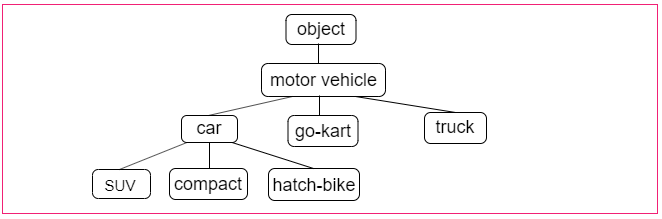 このグラフ構造だと、「car」の上位概念に「motor vehicle」という単語が、また「car」の下位概念に「SUV」などの具体的な車種があることが示されている。
このグラフ構造だと、「car」の上位概念に「motor vehicle」という単語が、また「car」の下位概念に「SUV」などの具体的な車種があることが示されている。
このように全ての単語に対して類義語の集合を作り、それぞれの関係をグラフ構造で表現することで、単語間のつながりを定義できる。
自然言語処理のアプリケーションにおいてシソーラスをどのように利用するかというと、例えば検索エンジンにおいて、「automobile」と「car」が類義語であることを知っていれば、「automobile」の検索結果を「car」の検索結果に含めることができる。
WordNetを使えば類義語を取得したり、「単語ネットワーク」を利用したりすることができる。また、「単語ネットワーク」を用いれば単語間の類似度を算出することも可能だ。
しかし既にお気付きの方もいるだろうが、このWordNetなどのようなシソーラスには、以下のような欠点がある。
時代の変化に対応することが困難 :
時とともに新しい言葉が誕生し、古い言葉は廃れていくように我々の使う言葉は「生きて」いる。
人の作業コストが高い :
例えば、現存する英単語は1,000万語を超えており、それぞれの単語に対し定義付けを行うには大幅な人件コストがかかる。
単語の細かなニュアンスを表現できない :
似たような単語であったとしてもそれぞれニュアンスは異なり、それを人間の手によって関連付けを行うのは至極困難。
このように、シソーラスなどの人手によって単語の意味を定義付けていく手法には大きな問題がある。
そこでこの問題を回避するために、続いて「カウントベースの手法」、ニューラルネットワークを用いた「推論ベースの手法【次回】」を紹介する。
これら二つの手法は、大量のテキストデータから自動的に「単語の意味」を抽出する、つまり、単語の関連付けに人が介入しなくても良いということだ。
このコーパスと呼ばれるデータは、自然言語処理の研究やアプリケーションのために目的を持って収集されたテキストデータである。
自然言語処理に関する分野で有名なコーパスといえば、WikipediaやGoogle Newsなどのテキストデータが挙げられる。
他方RGBの3成分がどれだけの割合で存在するかといった方法でも色は表現できる。つまり色を3次元のベクトルとして表現できるということである。
注目すべき点はRGBのようなベクトル表現の方がより正確に色を表現、指定できるということである。例えば先の飴色のようにどういう色なのか想像できない場合、飴色のRGBは(R, G, B)=(144, 103, 62)と表現できるので、明るい茶色っぽい感じがわかる。
また、色同士の関連性もこのベクトル表現の方が容易に判断しやすく、定量化も行えるので便利である。
このようなベクトル表現を、今議論している「単語」についても行えないだろうか?我々の目指すべきゴールは「単語の意味」を的確に捉えたベクトル表現である。
これは自然言語処理の分野では、単語の分散表現と呼ばれる。
自然言語処理の歴史において、単語をベクトルで表す研究は今まで数多く行われてきたが、その重要な手法の殆どがあるアイデアに基づいていることが分かる。
それは『単語の意味は、その周辺の単語によって形成される』という非常にシンプルなものである。
これは、分布仮説 (distributional hypothesis) と呼ばれている。つまり単語自体には意味がなく、その単語の「コンテキスト(文脈)」によって単語の意味が形成されるということだ。
例えば、「I drink water.」「You drink coffee.」などのように「drink」という単語の近くには飲み物が現れやすい。
また「I guzzle water.」「You guzzle coffee.」などの文章から、「drink」「guzzle」の意味は近そうだといった具合である。(guzzle: ガブガブ飲む という意味)
本記事では「コンテキスト」と言うとき、注目する単語に対してその周囲にある単語のことを指す。またコンテキストのサイズを「ウィンドウサイズ」という言葉で表すことにする。
例えばウィンドウサイズ2の場合、
といったように、「goodbye」に注目したときその左右の2単語をコンテキストとして利用する。
そのための素直な方法は、周囲の単語をカウントする「カウントベースの手法」である。
具体的には、或る注目している単語に対して、その周囲にどのような単語がどれだけ現れているのかをカウント、集計するのである。
では実際に、先の"You say goodbye and I say hello."という文章について、そのコンテキストに含まれる単語の頻度をカウントしていこう。ウィンドウサイズは1とする。
この文字列には全部で7つの単語(ピリオド含む)が含まれており、「You」という単語は[0, 1, 0, 0, 0, 0, 0]とベクトル表記できることがわかる。
なぜならばウィンドウサイズを1としているので、「You」の周辺単語は「say」のみであり、「say」にのみコンテキストの目印として共起した回数の1をカウントしているからである。
次に「say」については文字列中に2回現れていることに注意すると、[1, 0, 1, 0, 1, 1, 0]とベクトル表記できる。これらの作業を7つの単語について全て行うと、次のようなテーブルが得られる。
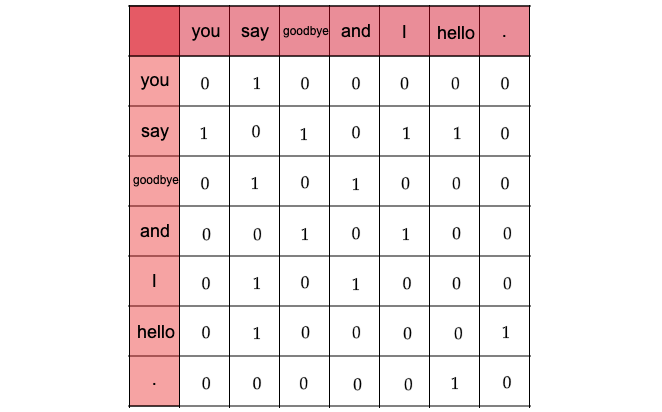 このテーブルの各行が、該当する単語のベクトルに対応している。これは行列の形に対応していることから 共起行列と呼ばれている。
このテーブルの各行が、該当する単語のベクトルに対応している。これは行列の形に対応していることから 共起行列と呼ばれている。
ここでは手動で共起行列を作成したが、もちろんこれはpythonなどを用いて自動化でき、コードはGithub上に上がっているので参照してもらいたい。
ベクトル間の類似度を計測するのには、ベクトルの内積、ユークリッド距離などが代表例としてあげられるが、単語のベクトル間類似度を計測する際は コサイン類似度が主に使われる。コサイン類似度は以下の式で定義される。
\(\boldsymbol{x}=(x_1, x_2, \cdots ,x_n ), \boldsymbol{y}=(y_1, y_2, \cdots ,y_n )\)とした時、
$$ sim_{cos} = \dfrac{\boldsymbol{x} \cdot \boldsymbol{y}}{|\boldsymbol{x}| |\boldsymbol{y}|} = \dfrac{x_1 y_1 + x_2 y_2 + \cdots + x_n y_n}{\sqrt{x_1^2 + x_2^2 + \cdots + x_n^2} \sqrt{y_1^2 + y_2^2 + \cdots + y_n^2}} $$ 分子にベクトルの内積、分母に各ベクトルのL2ノルムの積を取っている。
注目すべきポイントはベクトルを正規化してから内積を取っているということである。2つのベクトルが同じ向きを向いているときにコサイン類似度は1、完全に反対向きだと-1になることは直感的に分かるだろう。
しかし、カウントベースの手法(特に共起行列の部分)には様々な改善点があり、今回はその改善点について取り組んでいくことにする。
しかしこの回数は実際あまり良い性質を持っていない。というのも、例えばあるコーパスにおいて「the」と「car」の共起を考えてみることにする。「the」は冠詞なので「...the car...」などというフレーズは多数あり、共起回数は必然的に大きくなる。
他方、「car」と「drive」は明らかに強い関係があるが、「...drive car...」というフレーズの出現回数は低いと予想できる。つまり、単に共起回数だけを見てしまうと「drive」よりも「the」のほうが強い関連性があると評価してしまうことになる。
こういった問題を解決するために、 相互情報量(PMI) という指標が使われる。これはX、Yという確率変数に対して次の式で定義される。
$$ PMI(X,Y) = \log_2 \frac{P(X,Y)}{P(X)P(Y)}$$ このPMIの値が大きいほど関連性が高いことが示される。
この式より、単語単独の出現回数が考慮されたことになるので良い指標と言えそうだ。
しかし、このPMIの式には1つ問題がある。それは、2つの単語で共起する回数が0となるとき\(PMI =\log_2 0 = -\infty\)となってしまうことである。それに対応して、実際によく使われるのは次の 正の相互情報量(Positive PMI:以降PPMIと書く) である。
$$ PPMI(X,Y) = max(0, PMI(X,Y))$$ これは、PMIがマイナスのときは0を返す関数と見ることができ、単語間の関係性を0以上の実数値として表している。
これによって共起行列をPPMI行列に変換できるのだが、このPPMI行列にも大きな問題がある。例えば語彙数100万のコーパスを扱うとなると、ベクトルの次元数も必然的に100万にまで及び、このベクトルをそのまま用いるのは現実的でない。
さらに、PPMI行列の要素を見てみるとその多くが0であることが分かる(疎な行列)。これはベクトルの殆どの情報が重要ではない、つまり各要素の持つ重要度は低いと言える。このようなベクトルはノイズに弱く、頑健性に乏しいため次に説明する次元削減を行うのが一般的である。
次元削減を行う方法はたくさんあるが今回は特異値分解(SVD)を使った次元削減を行う。SVDは任意の行列を3つの行列の積として表せる。数式で書くと、
$$ X = \boldsymbol{US}\boldsymbol{V}^{T} $$ ここでUとVは直交行列でありその列ベクトルは互いに直行する。またSは対角行列である。
これらを視覚的に表すと次のようになる。(薄緑の部分にそれぞれ要素の値が入る)
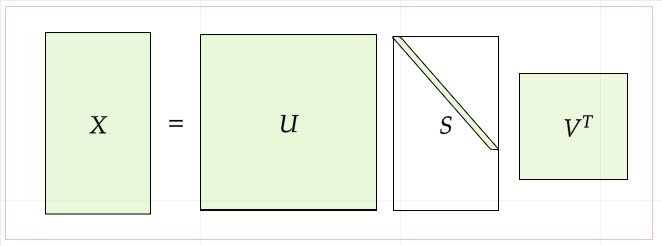 さて、上式においてUは直交行列であったがこの直行行列は何らかの基底を形成している。
さて、上式においてUは直交行列であったがこの直行行列は何らかの基底を形成している。
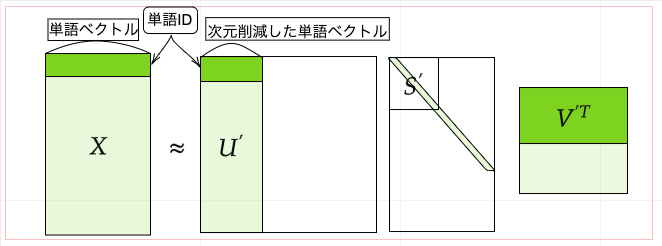
つまりUという行列を単語空間として扱うことができる。またSは対角行列であり、その対角成分には特異値が大きい順に並んでいる。特異値は対応する基底の重要度とみなすことができる。つまり以下のように重要でない要素を削ることができるのである。
 Wikipedia
Wikipedia
ゼロから学ぶDeep Learning2
※内容はオーム社『ゼロから学ぶDeep Learning2』を参考にしている
目次
1. はじめに:自然言語処理(NLP)とは
2. シソーラスによる手法
3. カウントベースの手法( 統計的手法 )
4. カウントベースの手法の改善点
5. 【次回】word2vec( ←これがメイン )
6. まとめ
7. 参考文献
1.はじめに:自然言語処理(NLP)とは
まず一般に 自然言語 (Natural Language)とは、人間によって日常の意思疎通のために用いられる、文化的背景を持って自然に発展してきた言語(日本語、英語、中国語など)である。そこで 自然言語処理 (Natural Language Processing: NLP )とは、一言で言うと「我々が普段用いてる言葉をコンピュータに理解させるための技術」である。
NLPの目標とするところは、人間が話す「同じような文章でも意味や表現が異なるような」言葉をコンピュータに理解させ、我々にとって有益なことをコンピュータに行わせることである。例えば機械翻訳、検索エンジン、文章の感情分析などが挙げられる。
我々の身の回りではそのような自然言語処理の技術がすでに数多く使われている。
我々の使う言葉は「文字」によって構成され、言葉の意味は「単語」によって構成されている。「単語」は、言わば意味の最小単位である。
つまるところ、自然言語をコンピュータに理解させるには、「単語の意味」を理解させることが重要であるといえそうだ。
そこで本記事では「単語の意味」をうまく捉えた表現方法について「シソーラス」による手法、「カウントベース」の手法の2つを見ていく。
2.シソーラスによる手法
「単語の意味」を表すためには、人の手によって単語の意味を定義することが考えられる。例えば『広辞苑』のように、ひとつひとつの単語に対してその単語の意味を説明することである。しかし自然言語の歴史を振り返ると、『広辞苑』のように人が使う一般的な辞書ではなく 、 シソーラス (thesaurus)と呼ばれるタイプの辞書が多く使われてきた。
シソーラスとは「類語辞書」のことで、「同義語」や「類義語」が同じグループに分類されている。例えば、「car」という単語に対して、
また、自然言語処理において利用されるシソーラスでは、単語間で「上位と下位(is a の関係)」、「全体と部分(part-of の関係)」などのより細かい関係性が定義されている場合がある。次のようなグラフ構造によって各単語の関係性が定義される。
 このグラフ構造だと、「car」の上位概念に「motor vehicle」という単語が、また「car」の下位概念に「SUV」などの具体的な車種があることが示されている。
このグラフ構造だと、「car」の上位概念に「motor vehicle」という単語が、また「car」の下位概念に「SUV」などの具体的な車種があることが示されている。このように全ての単語に対して類義語の集合を作り、それぞれの関係をグラフ構造で表現することで、単語間のつながりを定義できる。
自然言語処理のアプリケーションにおいてシソーラスをどのように利用するかというと、例えば検索エンジンにおいて、「automobile」と「car」が類義語であることを知っていれば、「automobile」の検索結果を「car」の検索結果に含めることができる。
WordNet
自然言語処理の分野において、最も有名なシソーラスは「WordNet」である。WordNetは1985年からプリンストン大学で開発がスタートされたシソーラスであり、様々な自然言語処理のアプリケーションにおいて大いに活躍してきた。WordNetを使えば類義語を取得したり、「単語ネットワーク」を利用したりすることができる。また、「単語ネットワーク」を用いれば単語間の類似度を算出することも可能だ。
しかし既にお気付きの方もいるだろうが、このWordNetなどのようなシソーラスには、以下のような欠点がある。
時代の変化に対応することが困難 :
時とともに新しい言葉が誕生し、古い言葉は廃れていくように我々の使う言葉は「生きて」いる。
人の作業コストが高い :
例えば、現存する英単語は1,000万語を超えており、それぞれの単語に対し定義付けを行うには大幅な人件コストがかかる。
単語の細かなニュアンスを表現できない :
似たような単語であったとしてもそれぞれニュアンスは異なり、それを人間の手によって関連付けを行うのは至極困難。
このように、シソーラスなどの人手によって単語の意味を定義付けていく手法には大きな問題がある。
そこでこの問題を回避するために、続いて「カウントベースの手法」、ニューラルネットワークを用いた「推論ベースの手法【次回】」を紹介する。
これら二つの手法は、大量のテキストデータから自動的に「単語の意味」を抽出する、つまり、単語の関連付けに人が介入しなくても良いということだ。
3.カウントベースの手法【統計的手法】
これからカウントベースの手法を説明していくが、ここでは「コーパス」と呼ばれる大量のテキストデータを用いる。このコーパスと呼ばれるデータは、自然言語処理の研究やアプリケーションのために目的を持って収集されたテキストデータである。
自然言語処理に関する分野で有名なコーパスといえば、WikipediaやGoogle Newsなどのテキストデータが挙げられる。
分散表現・分布仮説
さて、世の中には様々な「色」が存在するが、それらの色には「暗紅色」や「飴色」などの固有の名前が付けられている。他方RGBの3成分がどれだけの割合で存在するかといった方法でも色は表現できる。つまり色を3次元のベクトルとして表現できるということである。
注目すべき点はRGBのようなベクトル表現の方がより正確に色を表現、指定できるということである。例えば先の飴色のようにどういう色なのか想像できない場合、飴色のRGBは(R, G, B)=(144, 103, 62)と表現できるので、明るい茶色っぽい感じがわかる。
また、色同士の関連性もこのベクトル表現の方が容易に判断しやすく、定量化も行えるので便利である。
このようなベクトル表現を、今議論している「単語」についても行えないだろうか?我々の目指すべきゴールは「単語の意味」を的確に捉えたベクトル表現である。
これは自然言語処理の分野では、単語の分散表現と呼ばれる。
自然言語処理の歴史において、単語をベクトルで表す研究は今まで数多く行われてきたが、その重要な手法の殆どがあるアイデアに基づいていることが分かる。
それは『単語の意味は、その周辺の単語によって形成される』という非常にシンプルなものである。
これは、分布仮説 (distributional hypothesis) と呼ばれている。つまり単語自体には意味がなく、その単語の「コンテキスト(文脈)」によって単語の意味が形成されるということだ。
例えば、「I drink water.」「You drink coffee.」などのように「drink」という単語の近くには飲み物が現れやすい。
また「I guzzle water.」「You guzzle coffee.」などの文章から、「drink」「guzzle」の意味は近そうだといった具合である。(guzzle: ガブガブ飲む という意味)
本記事では「コンテキスト」と言うとき、注目する単語に対してその周囲にある単語のことを指す。またコンテキストのサイズを「ウィンドウサイズ」という言葉で表すことにする。
例えばウィンドウサイズ2の場合、

といったように、「goodbye」に注目したときその左右の2単語をコンテキストとして利用する。
共起行列
では、分布仮説に基づいて単語をベクトルとして表す方法を考えてみよう。そのための素直な方法は、周囲の単語をカウントする「カウントベースの手法」である。
具体的には、或る注目している単語に対して、その周囲にどのような単語がどれだけ現れているのかをカウント、集計するのである。
では実際に、先の"You say goodbye and I say hello."という文章について、そのコンテキストに含まれる単語の頻度をカウントしていこう。ウィンドウサイズは1とする。
この文字列には全部で7つの単語(ピリオド含む)が含まれており、「You」という単語は[0, 1, 0, 0, 0, 0, 0]とベクトル表記できることがわかる。
なぜならばウィンドウサイズを1としているので、「You」の周辺単語は「say」のみであり、「say」にのみコンテキストの目印として共起した回数の1をカウントしているからである。
次に「say」については文字列中に2回現れていることに注意すると、[1, 0, 1, 0, 1, 1, 0]とベクトル表記できる。これらの作業を7つの単語について全て行うと、次のようなテーブルが得られる。
 このテーブルの各行が、該当する単語のベクトルに対応している。これは行列の形に対応していることから 共起行列と呼ばれている。
このテーブルの各行が、該当する単語のベクトルに対応している。これは行列の形に対応していることから 共起行列と呼ばれている。ここでは手動で共起行列を作成したが、もちろんこれはpythonなどを用いて自動化でき、コードはGithub上に上がっているので参照してもらいたい。
ベクトル間の類似度
今、共起行列で単語をベクトル化することに成功したが、続いてベクトル間の類似度を計測する方法を見ていこう。ベクトル間の類似度を計測するのには、ベクトルの内積、ユークリッド距離などが代表例としてあげられるが、単語のベクトル間類似度を計測する際は コサイン類似度が主に使われる。コサイン類似度は以下の式で定義される。
\(\boldsymbol{x}=(x_1, x_2, \cdots ,x_n ), \boldsymbol{y}=(y_1, y_2, \cdots ,y_n )\)とした時、
$$ sim_{cos} = \dfrac{\boldsymbol{x} \cdot \boldsymbol{y}}{|\boldsymbol{x}| |\boldsymbol{y}|} = \dfrac{x_1 y_1 + x_2 y_2 + \cdots + x_n y_n}{\sqrt{x_1^2 + x_2^2 + \cdots + x_n^2} \sqrt{y_1^2 + y_2^2 + \cdots + y_n^2}} $$ 分子にベクトルの内積、分母に各ベクトルのL2ノルムの積を取っている。
注目すべきポイントはベクトルを正規化してから内積を取っているということである。2つのベクトルが同じ向きを向いているときにコサイン類似度は1、完全に反対向きだと-1になることは直感的に分かるだろう。
4.カウントベースの手法の改善点
さて、ここまでで我々は単語の共起行列を作れるようになり、それによって我々のゴールであった単語のベクトル化に成功した。しかし、カウントベースの手法(特に共起行列の部分)には様々な改善点があり、今回はその改善点について取り組んでいくことにする。
相互情報量(Pointwise Mutual Information)
先程も述べたように共起行列の要素は、2つの単語が共起した回数を表している。しかしこの回数は実際あまり良い性質を持っていない。というのも、例えばあるコーパスにおいて「the」と「car」の共起を考えてみることにする。「the」は冠詞なので「...the car...」などというフレーズは多数あり、共起回数は必然的に大きくなる。
他方、「car」と「drive」は明らかに強い関係があるが、「...drive car...」というフレーズの出現回数は低いと予想できる。つまり、単に共起回数だけを見てしまうと「drive」よりも「the」のほうが強い関連性があると評価してしまうことになる。
こういった問題を解決するために、 相互情報量(PMI) という指標が使われる。これはX、Yという確率変数に対して次の式で定義される。
$$ PMI(X,Y) = \log_2 \frac{P(X,Y)}{P(X)P(Y)}$$ このPMIの値が大きいほど関連性が高いことが示される。
この式より、単語単独の出現回数が考慮されたことになるので良い指標と言えそうだ。
しかし、このPMIの式には1つ問題がある。それは、2つの単語で共起する回数が0となるとき\(PMI =\log_2 0 = -\infty\)となってしまうことである。それに対応して、実際によく使われるのは次の 正の相互情報量(Positive PMI:以降PPMIと書く) である。
$$ PPMI(X,Y) = max(0, PMI(X,Y))$$ これは、PMIがマイナスのときは0を返す関数と見ることができ、単語間の関係性を0以上の実数値として表している。
これによって共起行列をPPMI行列に変換できるのだが、このPPMI行列にも大きな問題がある。例えば語彙数100万のコーパスを扱うとなると、ベクトルの次元数も必然的に100万にまで及び、このベクトルをそのまま用いるのは現実的でない。
さらに、PPMI行列の要素を見てみるとその多くが0であることが分かる(疎な行列)。これはベクトルの殆どの情報が重要ではない、つまり各要素の持つ重要度は低いと言える。このようなベクトルはノイズに弱く、頑健性に乏しいため次に説明する次元削減を行うのが一般的である。
次元削減(Dimensionality reduction)
次元削減とは、ベクトルの次元を削減することに他ならないが、ベクトルの持つ「重要な情報」をできる限り保持した上で削減することがポイントである。次元削減を行う方法はたくさんあるが今回は特異値分解(SVD)を使った次元削減を行う。SVDは任意の行列を3つの行列の積として表せる。数式で書くと、
$$ X = \boldsymbol{US}\boldsymbol{V}^{T} $$ ここでUとVは直交行列でありその列ベクトルは互いに直行する。またSは対角行列である。
これらを視覚的に表すと次のようになる。(薄緑の部分にそれぞれ要素の値が入る)
 さて、上式においてUは直交行列であったがこの直行行列は何らかの基底を形成している。
さて、上式においてUは直交行列であったがこの直行行列は何らかの基底を形成している。つまりUという行列を単語空間として扱うことができる。またSは対角行列であり、その対角成分には特異値が大きい順に並んでいる。特異値は対応する基底の重要度とみなすことができる。つまり以下のように重要でない要素を削ることができるのである。
 Wikipedia
Wikipediaゼロから学ぶDeep Learning2



