はじめに
今回は2分類SVMについて見ていきますが、数学や機械学習の知識があまりない方も全体のイメージを掴めるよう数式を使うことを極力避けました。ですので厳密には間違っている表記もイメージしやすいよう、わざと入れていることを始めに断っておきます。
SVMを数式を追ってしっかりと理解したいという方には物足りない内容になっていると思いますがご了承ください。
SVMとは
SVMとは、教師あり学習を用いるパターン認識モデルの一つで、回帰、分類両方につかうことができます。ここでは2分類SVMを考えていきます。
SVMは、「マージン最大化」という考え方を用いて分類する境界(決定境界)を決めます。この考え方によって他の分類モデルよりも高い識別性能を実現していますが、その理由とともにマージン最大化を用いて、次の赤と青のクラスの分類について見ていきます。

ここでは簡単のために二次元で直線で分類することを考えますが、三次元以上になったときは下のように平面で切っていると考えてください。なので直線と出できたら基本的には平面に言い換えられると思ってください。

・マージン最大化
マージンとは、分類する境界とデータとの距離のことで、いくつも考えられる境界の中から、サポートベクトルという「分類する境界に一番近いデータ点(境界を決めるのに使うデータ)」との距離が最大となるような境界を見つけようというのがマージン最大化という考え方です。このとき、それぞれのクラスのサポートベクトルに対するマージンは同じであるとします。ただし、2クラスそれぞれのサポートベクトル間の距離をマージンということもありますが、結局その距離のちょうど半分にしたところに境界を設定しているということです。つまり、どちらでマージンを設定するにしろ、2つのクラスからなるべく離れたところに境界を引きたいということです。
マージン最大化の考え方を用いて赤と青の2つのクラスを分類してみると次のようになります。

では、なぜマージン最大化を用いて分類することで高い識別性能が得られるのでしょうか。
上の図のような分類を考えると、その分類する境界というのは無数に考えることができます。まず考えてほしいのは分類する目的の大前提として、今ある値を分類することにより、まだどちらのクラスの属するか分からない未知の値に対してどちらのクラスに属するかを正しく予測することがあります。つまり、分かっているデータに対して正しく分類できたところで、未知のデータに対しての正しく予測できている割合が極端に低くなるような境界では全くの無意味だということです。


例えば、図のように片方もしくは両方のクラスの値ギリギリにあるような境界を設定してしまうと、そこからほんの少しだけずれたようなデータに対して誤分類を起こしてしまう可能性が高くなります。そこで、マージン最大化を考えることにより、データが少しずれただけでは誤分類を起こさなくなります。これによりマージンを考えて決めた境界で分類することにより、それを考えずに境界を決めたモデルより「汎化能力(新しいデータに対して正しく予測する能力)」が高くなっています。このことから、SVMはマージン最大化を考えることにより、汎化性能が最も高い境界により分類を行うことを可能にしています。
・ソフトマージン
ここまでは、2クラスに対して直線で分類可能(線形分離可能)なデータに対して考えてきましたが、データが次のようになっていたらどうでしょう。

データがこの様になっていた場合、直線で2クラスを完全に分類するのは不可能です。このようなデータに対して完全に分類しようとすると、もし誤分類をしてしまったデータに分類に大きく影響するような情報が含まれていた場合、汎化能力が下がってしまいます。ここで出てくるのがソフトマージンです。
実は先程までの、線形分離可能なデータに対して考えたマージンをハードマージンといい、これは完全に2つのクラスを分類できることを前提にしたマージンです。それに対してソフトマージンは、あらかじめ誤分類を許すことで汎化性能を高めることを考えたマージンです。もちろん、誤分類が多すぎては汎化性能を高めるどころか低くしてしまう一方なので、「境界線とデータがなるべく離れていること」・「誤分類数をなるべく少なくすること」の2つを達成するようにします。
そこで次のような値を最小にすることを考えて、境界を決めます。

ここでCは、「どの程度まで誤分類を許すか」を表すパラメータです。Cが小さい場合、多少誤分類数が多くても値は大きくならないので、ある程度誤分類を許すことになります。それに対して、Cが大きい場合、誤分類数がより0に近くなければ値が大きくなってしまうので、あまり誤分類を許さないことになります。Cが無限に大きければ誤分類を許さなくなるので、上でのハードマージンと一致します。つまりCの大きさを調整すればハードマージン・ソフトマージンの両方を実現することができるので、C-SVMで両方の問題に対応できます。
C-SVMで分類した様子は次のようになります。

ここで、なんでマージン境界内に点が入ってくるのか、なんでサポートベクトルが色々増えているのかと思ったと思います。実は上で書いた式に少しだけ嘘が含まれていて、そこは誤分類数のところです。ここの値はダイレクトに誤分類数を表しているのではなく、誤分類したデータやマージン境界内にあるデータによって決まる値なんです。詳しく言うと、マージン境界より外で正しく分類できている点に対しては0、マージン境界内で正しく分類できるデータに対しては0から1の間の値、誤分類している値に対しては1より大きな値を与えます。なので、境界を決める際に誤分類のデータとマージン境界内のデータにより決めていることになります。そこでサポートベクトルの定義に戻ると、境界を決めるのに使う(影響のある)データなので、今までは境界から一番近いデータ(紫)がそれになっていましたが、ここではそれ以外にもマージン境界内のデータ(緑)と誤分類をしたデータ(黄色)が使われるのでそのデータもサポートベクトルになっているのです。そのそれぞれにも名前がついていて、マージン境界上のデータ(紫)が自由サポートベクトル、それ以外のサポートベクトル(黄・緑)を上限サポートベクトルといいます。実際にはこんな値が入りますが、結局一番影響を与える誤分類数をCでどの程度にするのかが一番重要ですので、そこをまずは抑えて、境界を決める要素が増えたんだなーと思っていいただければいいと思います。

ソフトマージンにより非線形分離不可能なデータに対してSVMを適用できましたが、ここでのCは自分で決めなければならず、まず最適なパラメータを見つける必要があります(これがSVMの欠点につながる)。ここでは詳しいことは述べませんが、その方法としてグリッドリサーチ(色々なパラメータを試して精度の良いものを採用する)などがあります。
・カーネルトリック
ソフトマージンにより、直線で分離が不可能な場合でも誤分類により境界を決定することができましたが、直線で分離をしているので、ある程度の性能しか望むことができません。そこで登場するのがカーネルトリックです。この手法によりSVMは強力な威力を発揮します。
この手法を考えるときに次のような2クラスを分類することを考えます。

これを分類しようとしたときに、今まで出てきたSVMを使ってやろうとしてもうまくいかないだろうと思うはずです。そこで、直線だけでなく曲線を使えるとしたら、下のような境界を使って分類することができれば良いですよね。

この境界を引くことをできるようにしたのがカーネルトリックです。
では、どのようにこれを可能にしているのかを数式は使わず考え方を中心に説明します。参考書なんかを見ると特徴空間に変換して分類するみたいなことが書いてあると思います。これは、今ある特徴量(上の赤と青の位置を決めているもの)では分類できないものを、新しい特徴量を作って分類できるようにしようということです。
※特徴量のイメージをしやすいように、予測の流れを出しときます。

ここでのカーネルのイメージとしては、直線で分類できないものを、マージン最大化の最初で出てきたようなデータがある程度分かれた状態にして、直線で分類できるようにするというものです。これを簡単な例で見ていきましょう。
次のようなデータが数直線上にあったらどう頑張っても直線では赤と青のクラスに分けるごとができません。

そこで二乗した値を作るとどうでしょう。

すると、このように直線で分類することができるようになります。厳密に言うと違うのですが、イメージ的にはこのような変換をカーネルで行います。実はカーネルにも種類があって代表的なのはガウスカーネルと多項式カーネルですが、ここでは主にガウスカーネルについて考えていこうと思います。
ガウスカーネルは簡単に言うと値と値の近さを表しているものです。例を見るとイメージが掴めると思うので、円の境界を引きたいと思った例で考えてみましょう。
この例では感覚として、真ん中らへんとその周りに分けることを考えたと思います。その感覚で真ん中らへんとそれ以外をはっきり分けられるような特徴量を今あるデータ(特徴量)から作れないかなーと考えるわけです。そこでガウスカーネルによって特徴量を考えていきますが、近くにあるデータは似た特徴量を持っていてほしいじゃないですか。例えば真ん中らへんにあるデータに対しては小さいけど、周りにあるデータに対しては大きい特徴量があれば、下のようになって分類しやすくなります。

ガウスカーネルはデータとデータの近さを基準としてこの変換を行います。まずある一点を基準として、他のすべてのデータとの近さに関する値を出します。これを、基準を変えてすべてのデータ間の近さを調べて、それを使った値を特徴量として変換を行います。ここでどのくらいの近さまでを同じクラス、似た特徴量を持ったとするのかという問題が起きます。これを決めるのにはカーネルの中にあるパラメータを決めて調整しなければいけません。ただ、基本的には近さでデータの特徴を決めたいんだということだけまずは理解してほしいです。
分かりやすいように、3つのデータだけで考えてみましょう。それぞれの点からの距離を取って、ある点からAまでの距離を特徴量a、Bまでの特徴量をb、Cまでの特徴量をcとします。実際は今あるデータの特徴量を使ってガウスカーネルで変換しますが、ここでは簡単のため距離をそれぞれ設定しました。

ここで、特徴量a、b、cをそれぞれの点でみると、CだけA、Bとは逆(A,Bからの距離が近いときはCは遠い)になっていることが分かると思います。つまり、クラスの違うCだけが仲間はずれとなっています。こういったことを、もっとデータ数が多くて、直線で分類できない問題に対してカーネルを使って変換することでやっているのがカーネルトリックです。多項式カーネルは、意味としては最初に二乗した例に近いことがあるかもしれませんが、やりたいことは同じです。
では、元の例に戻ってカーネルで変換する様子の一部分見ると次のようになります。

このように特徴量を変換するとイメージとしては次のようになり、分類が明らかにしやすい配置になっているのが分かると思います。

まとめると、直線で分類できないものをカーネルを使ってデータの特徴量を、クラスの違う特徴量に変えて直線で分類しているということです。特徴量を変換したあとは、マージン最大化で分類をするので、上のカーネルを使わなかった分類と同じです。では、どのようにしてカーネルのある無しを使い分けたらいいのかを見ていきましょう。
・カーネルのある無しの使い分けとSVMの欠点
上のカーネルを使わないSVMと使うSVMを比べたとき、一見カーネルを使ったほうがそのままだと直線で分類できてものも分類できるからそっちを使えばいいと思うかもしれません。しかし、カーネルを使うのにも欠点があります。カーネルはより良い特徴量を取るために変換を行いましたが、もうすでに十分多くの特徴量が得ることができていたらどうでしょう。色んな特徴量があればそれだけ問題は複雑になるので、更にそこから変換を行うと今あるデータに厳密に従いすぎてしまいます(過学習という)。つまり新たなデータに対して無意味な境界になってしまうので、この場合はカーネルを用いないSVMを使ったほうがいいです。
逆に、特徴量が少ない場合、つまり十分な特徴量は得られない場合はどうでしょう。この場合はデータが非常に単純な場合を除いて、上で見てきたようなような直線で分類できないような問題になっている可能性が高いので、カーネルを用いたSVMを使うといいです。
ただ、データがかなり多い場合はカーネルを使うと、変換をするときに計算量が多くなってしまうので、この場合は変換をするのではなく特徴量を自分で増やして、十分にとってからカーネルを用いないSVMを使うといいです。
また、SVMの欠点としてはパラメータを設定しなければならなかったり、カーネルを選ばなければならないことや。データが多いときはあまり効率的ではありません。この問題をクリアしている手法として「ランダムフォレスト」があります。これを使えばSVMより効率よく良い結果が得られるかもしれませんが、これは実際に使ってみないとどちらの手法が良いのかは判断できませんし(どちらにも長所・短所がある)、それぞれの特徴をしっかり理解することが重要です。
まとめ
今回は2分類SVMについてやりました。数式をほとんど使わなかったので、逆に分かりづらいところもあったかもしれませんが、SVM全体のイメージは掴めたでしょうか。SVMは他にも1クラスに対して外れ値を検出するものや、回帰にも使えますし、ロジスティック回帰との関係を見ても面白いと思います。また、最後に出てきたランダムフォレストについては、他の記事を見てもらうと良いと思います。
参考文献
Logics of Blue サポートベクトルマシンの考え方
はじめてのパターン認識 平井有三(著) 森北出版











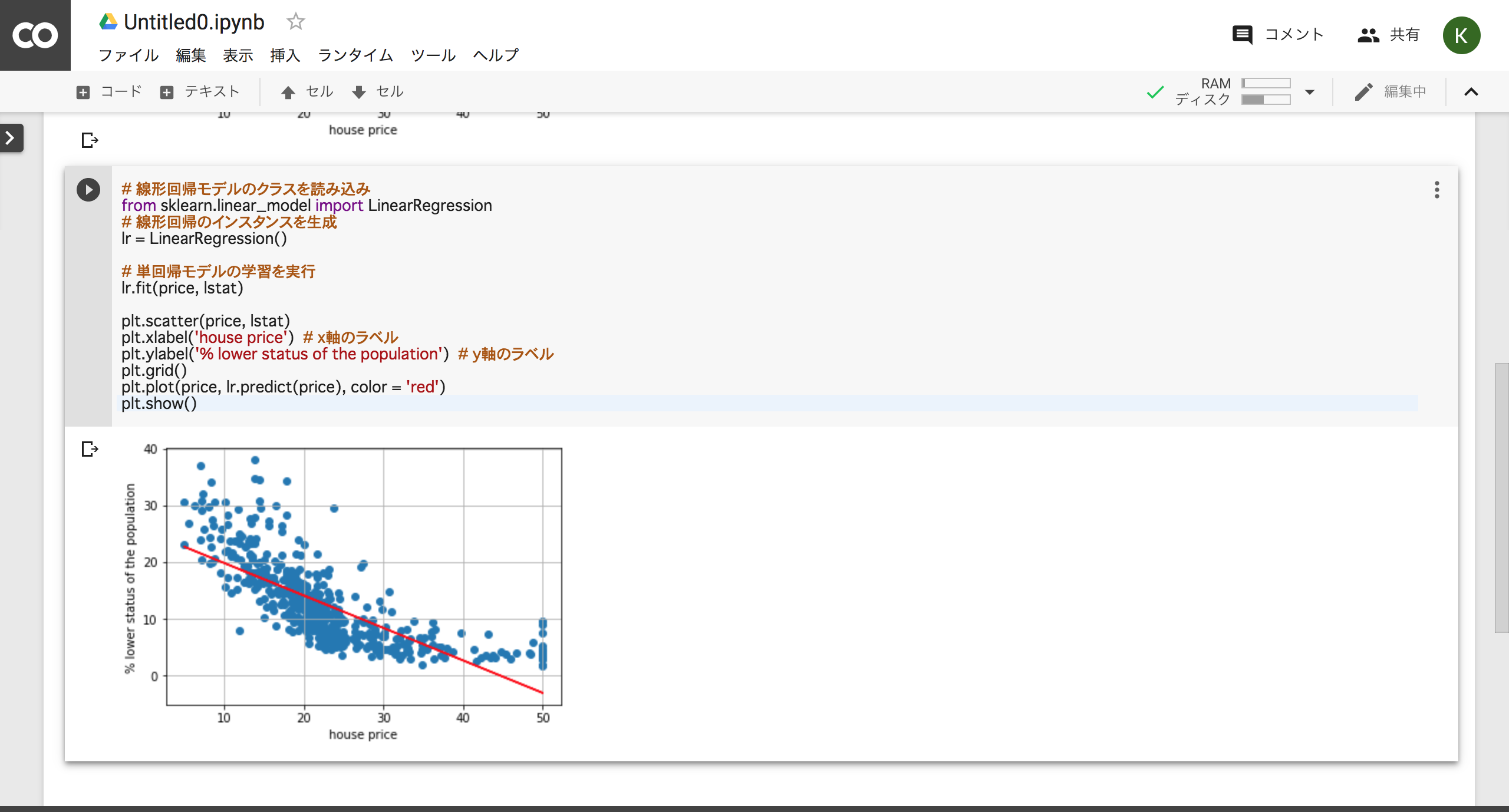
 が与えられた時、それと相関関係のあるyの値を説明、予測することである。ここで変数xを 説明変数 、変数yを 目的変数と呼ぶ。p=1、つまり説明変数が1つの時を単回帰、またp>=2、つまり説明変数が2つ以上の時を重回帰と呼ぶ。
が与えられた時、それと相関関係のあるyの値を説明、予測することである。ここで変数xを 説明変数 、変数yを 目的変数と呼ぶ。p=1、つまり説明変数が1つの時を単回帰、またp>=2、つまり説明変数が2つ以上の時を重回帰と呼ぶ。

 とはならないことに留意せよ。
とはならないことに留意せよ。







 を得るので、
を得るので、

 を通ることがわかる。
を通ることがわかる。



 と書くことにする。
と書くことにする。