概要

　はじめまして。アクセルユニバースのインターンに参加してる宇田川と申します。機械学習において必須の知識である数理モデルについて、その中でも特に基本的な回帰モデルに関して書いていこうと思います。

　このブログは機械学習を始めたばかり、または興味を持ち始めたばかりの方にわかっていただくようにわかりやすく書きました。事前知識としては機械学習の知識はもちろん必要なく高校数学における数学Bの確率の範囲程度の知識があれば十分です。よって細かい数式を書くことは避けました。回帰モデルのイメージを掴んでいただけたら幸いです。

その他のMicrosoft Azure Machine Learning Studioでやってみた記事も参考にしてください！
決定木アルゴリズムCARTを用いた性能評価
ロジスティクス回帰を用いた Iris Two Class Dataの分類
分位点回帰を用いた飛行機遅延予測
ランダムフォレスト回帰を用いた人気ブログタイトル予測

回帰モデルとは

　回帰モデルの説明をする前に回帰の語源について簡単に説明します。
回帰という言葉は英語でregressionと書きます。この言葉は遺伝学者であり統計学者でもある19世紀のフランシス・ゴルトンによって造られました。ゴルトンは、背の高い祖先の子孫の身長が必ずしも遺伝せず、平均値に戻っていく、すなわち「後退（＝regression）」する傾向があることを発見しました。これを「平均への回帰」といいいます。ゴルトンはこの事象を分析するために回帰モデルを発明しました。この発明が後に統計学の基礎となり回帰という言葉が誕生しました。

　では、回帰モデルについて書きましょう。回帰モデルとは関数をデータに適用することよって、ある(未知の、予測したい)変数yの変動を別の(既知の、予測するための)変数xの変動により説明・予測するための手法です。ここで登場した、説明したい変数yのことを目的変数、説明するために用いる変数xを説明変数と呼びます。説明変数xの数によって、1つであれば単回帰、2つ以上あれば重回帰という名前がついています。例として目的変数「頭の良さ」に対して、説明変数「大学の偏差値」のみで行うのが単回帰となり、目的変数「頭の良さ」に対して説明変数「コミュニケーション力」、「判断力」、「年齢」、「大学の偏差値」...と複数の説明変数を用いる場合が重回帰になります。

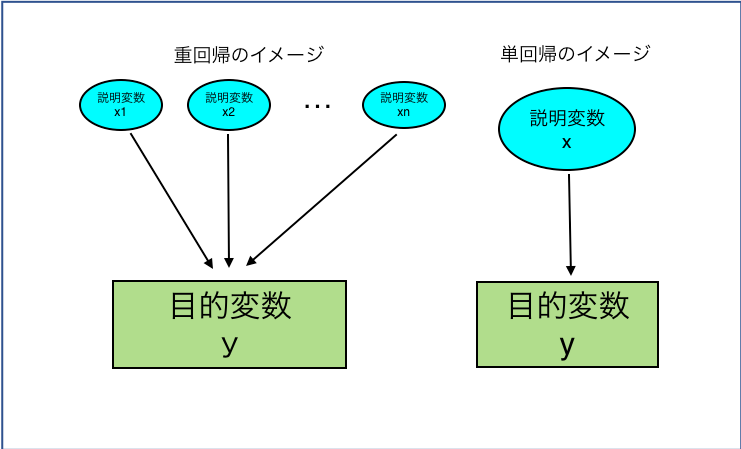
1. 単回帰

　単回帰は先ほど説明したように説明変数xが一つになるので式で表すとy=ax+b(aは係数、bは定数項です。a,bをパラメータや回帰係数と言ったりします。a,bを上手に決めると目的変数yの予測がうまくできます。後ほど少し詳しく書きます。)の形になり直線によって目的変数yを予測するモデルとなります。もちろん直線によってyを予測することになってしまうので単回帰のみで分析することはほぼありません。単回帰によって大まかな予測することで大まかな推測ができその後、他のモデルによって精度よく分析をします。単回帰は式がとてもシンプルなので簡単に大まかな予測ができます。

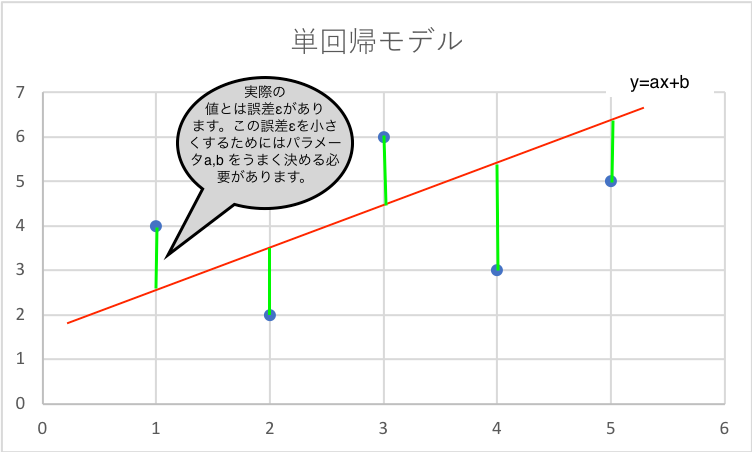
上の図からわかるように真の値と予測をしたyの値では誤差(上の図の緑線)が生じてしまいます。この誤差をεで表すと、先程のy=ax+bという式はy=ax+b+εと表せます。つまり、ε=y-ax-bとなり、この誤差は小さくしなければ良い予測ができたとは言えません。この誤差εを最小にするためのパラメータa,bを決めるのに有名な方法として最小２乗誤差法があります。最小２乗誤差法を説明をすると数学的になり数式が増えてしまうのでここではやめておきます。詳しく知りたい方は こちらのスライド21枚目を参考にしてみて下さい。ここではすでにわかっているn個の(x,y)の組(訓練データといいます。)を用いて最小２乗誤差法により最適なパラメータβ1,β0を求めています。

2. 重回帰

　重回帰は説明変数xが2つ以上になるので式で表すと、説明変数xがn個(x₁,x₂,...,xn. nは2以上)ある時、y=a₀+a₁x₁+a₂x₂+...+an*xn(a₀,a₁,...,anはパラメータ)の形になるのでn種類のxの変数によって目的変数yを予測することができます。説明変数が増えるので単回帰よりも予測の精度が高いのは明らかですね。

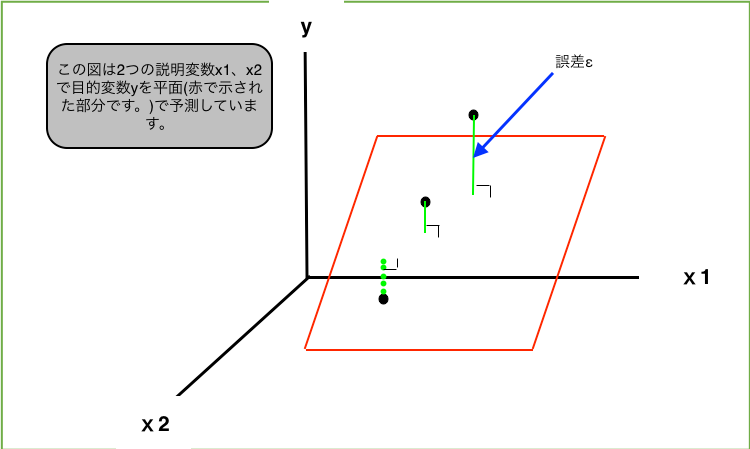
また重回帰の場合もパラメータa₀,a₁,...,anを誤差が小さくなるように考える必要があり、この場合も最小２乗誤差法が使われています。ここでも詳しく知りたい方は こちらを参考にしてみて下さい。パラメータα,β1,β2,...,βkを求めるために訓練データ(x,y)を用いて計算をしています。

　重回帰の実用例を挙げましょう。

カフェをこれから経営する予定のjさんがいると仮定します。

(1)これからjさんはどのくらい売上が成り立つのか知りたいと考えました。まずは、目的変数を決定します。この例では、目的変数は売上高です。

(2)ｊさんはカフェを経営するために売上高に関連しそうなデータを収集する必要があります。売上高を予想するには、都市人口、競合店舗、店舗面積、座席数、従業員数、メニュー数、利益率、広告費(説明変数です。)などのデータが必要です。目的変数が決まった後に説明変数を決定します。

(3)これらのデータが目的変数を出すのに必要なのか否か検討する必要があります。説明変数のデータの精度を上げるにはステップワイズ法で最適なデータを探します。ステップワイズ法は、はじめに最も有効な説明変数を1個採用する。その後まだ採用されていない説明変数の内で最も有用な説明変数を1個採用します。これを繰り返し行うが最初の方で採用された説明変数も不要になる場合があるので採用された変数を取り除くかどうかを確認する方法です。

(4)以上のものを使い方程式に落とし込むと

Y＝0.35✕店舗面積＋0.33✕座席数＋0.55✕従業員数.....＋0.77

売上高　　回帰係数　　回帰係数　　回帰係数　　　　　定数項

(数字は例です)

定数項は説明変数の影響を受けないベースの売上高の事です。

(5)この数式をを元にｊさんは売上高を高める方法として説明変数の寄与率の高いものに予算を多めに配分して寄与率の低いものは予算の配分を少なくするなどの調整を行います。

このようにして重回帰は利用されます。

3. ベイズ回帰

　単回帰、重回帰(まとめて線形回帰と呼びましょう。)では最小２乗誤差を求めてパラメータを決めていました(パラメータを推定するとも言います)。ベイズ回帰は線形回帰を確率の問題に読み替えることにしました。つまり、最適なパラメータを求めるということは一番高い確率になるパラメータを求めるということになります。ではどのようにして一番高い確率になるパラメータを求めればよいでしょうか。答えはたくさんあるのですが一番シンプルな例として尤度を最大にすることを扱いましょう(これを最尤推定法と呼びます)。

　尤度(ゆうど)の説明からします。パラメータθの確率モデルP(X=x;θ)と、D={x₁,x₂,...,xn}というそれぞれ独立な実現値(実現値は統計的な用語でデータ x を変量 X の値と考えています。)の集合を考えます。尤度はモデルのもとでDが得られる確率のことという意味です。尤度を数式で表すとP(D;θ)=P(X=x₁;θ)×P(X=x₂; θ)×...×P(X=xn;θ)と書けます。

　少し余談ですが、この式は確率を表す式的には何も変わりません。では尤度と確率は何が違うでしょうか。それは、式で表している意味合いが異なります。確率はこれから起きる可能性のあること(事象といいます。)それぞれがどれくらいの割合で起きるのかを表します。一方、尤度とはすでに観測されている(訓練データと呼んでいましたね。)起きてしまったデータの確率を考えています。

　余談はこれくらいにして最尤推定の説明をしましょう。最尤推定は尤度P(D;θ)を最大にするパラメータθを求めることです。このθを求めるときにP(D;θ)が積の形になると扱いづらいので両辺に対数をとって和の形にしたものlogP(D;θ)=logP(X=x₁;θ)+logP(X=x₂; θ)+...+logP(X=xn;θ)を対数尤度と言い、最尤推定を求めるときは対数尤度から求めるのが一般的です。

　ではこれを線形回帰において考えるとどうなるでしょうか。ここでは数式をたくさん書くのは避けて結果だけ書きます。先程のパラメータθに当たるところを単回帰ではa,b、重回帰ではa₀,a₁,...,anと考えて、訓練データ(x,y)においてある組(x,y)に対する誤差εがε~N(0,σ²)(これはどの組(x,y)に対しても誤差εが平均E(ε)=0、分散Var(ε)=σ²となり、またある２つの組(x,y)の誤差をε、ε'とするとその共分散Cov(ε,ε')=0と仮定しています。すると誤差εは平均0、分散σ²の正規分布に従うという意味です。このような分布を事前分布と呼んでいます。)として、最尤推定法により計算をしていくと最小２乗誤差法と同様の式が出て最適なパラメータの値は等しく推定することができます。

　ではベイズ回帰ではなぜ確率で考えるという手間を踏んでいるのでしょう。色々なメリットがありますが、簡単なメリットを挙げると、事前分布を考えて推定することができる点です。事前分布は私達がすでにわかっている知識などを考慮し分布を決め打ちするのが通常です。このように私達の知識を推定の中に取り入れられることです。

最後に

　今回は回帰モデル、特に基本的な3つの回帰モデルを書きました。単回帰では式がシンプルである一方、誤差が大きく良い推定ができませんでした。それを克服したのが重回帰でした。重回帰は誤差が小さく良い推定ができる一方、式が複雑になってしまいました。またベイズ回帰では事前分布を考えることにより私達の事前知識を数式に取り入れることができました。このように基本的な３つの回帰モデルにはメリット・デメリットがありました。今後、新たなモデルを学ぶ上でも３つの回帰モデルは重要になるので必ず理解しましょう。次回は、今回の基本的な回帰モデルと同じくらい重要なニューラルネットワークについて書きます。

参考文献

機械学習をはじめよう　第12回　ベイズ線形回帰［前編］

Pythonでベイズ線形回帰を実装してみた

回帰分析(単回帰分析)をわかりやすく徹底解説！

尤度とは何者なのか？