DEVELOPER’s BLOG
技術ブログ
海洋エネルギー × 機械学習〜機械学習を利用した電力需要量予測による波力発電の制御〜
〜普及に向けた課題と解決策〜に続き
私が前回作成した記事である「海洋エネルギー × 機械学習 〜普及に向けた課題と解決策〜」では、海洋エネルギー発電の長所と課題とその解決策について触れた。今回はそこで取り上げた、
繰り返しにはなるが、この「発電量・電力需要量予測」と「機械学習を用いた制御」とは、まずカレンダー条件（時間帯、曜日など）と気温や日射強度などの気象条件を説明変数として電力需要量を予測し、電力需要量の送電にかかる時間分先の予測値と同量を発電するように発電装置を制御するという、極めて単純な制御である。前提として、電力は常に需要量と供給量（発電量）が同量でなければ、停電を起こしてしまうのであるが、この制御を行えば、需要と供給のバランスを常に保ちながら発電することができる。また発電装置の無駄な待機時間も削減され、設備稼働率も向上する。このようにして、課題①「電力需要量とのバランスが取りにくい」、課題③「無駄な待機運転の時間がある」を解決するのである。今回は発電方法を波力発電としてこれを実装する。
目次
- 今回の実装の設定
- 機械学習による電力需要量の予測
- 並進動揺型の波力発電装置の運動制御
- 考察
- 参考文献
1. 今回の実装の設定
1-1. どんな波力発電装置で実装するか
まず波力発電装置の種類は表1、図1のように分類できる。
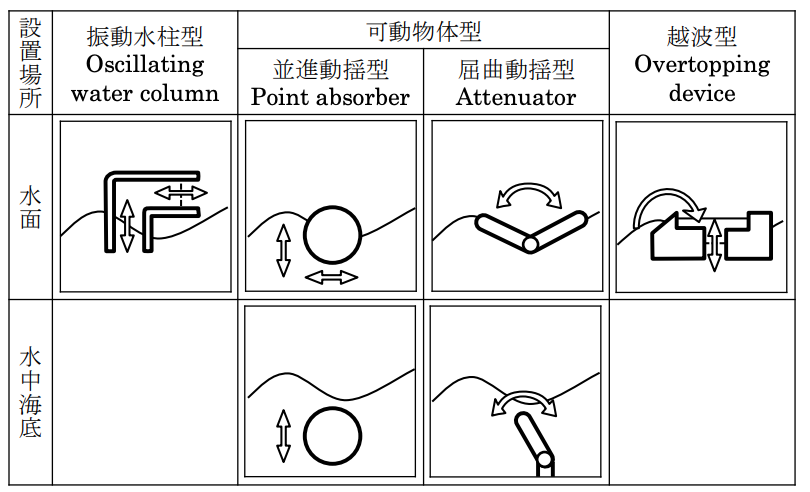
今回の実装では、垂直（上下）にのみ変位する並進動揺型の波力発電装置を考える。並進運動型の波力発電装置の特徴は、
- 波に対する指向性がなく、他の発電装置に対して波向きの影響の点から優位である
- 構造がシンプルで発電機構（PTO: power take off)も含め大部分が水中に没しているので、浮体本体の構造安全性や信頼性の点で有利である
- 波浪荷重、発電荷重を下端で支えているため繰り返しの係留力が作用することになり、下部の構造強度に配慮する必要性がある
- 発電装置が水面より下側にあることから、上部からの浸水に対しては十分注意が必要
また、現在最も実用化に近いものと見られる波力発電装置は、米国のOcean Power Technologies社が開発した並進動揺型の波力発電装置「PowerBuoy」（図2）である。
1-2. 実装の設定
2. 機械学習による電力需要量の予測
ある一軒家の電力需要量（電力使用量）を予測する時、本来ならば上記に示したようにカレンダー条件と気象条件を説明変数とするべきだが、カレンダー条件と気象条件、電力消費量のデータセットを手に入れることができなかったので、今回は特徴量を表3のようにしたデータセット（表4）を用いる。これは2016年1月11日17時00分から2016年5月11日16時50分までのデータセットである。
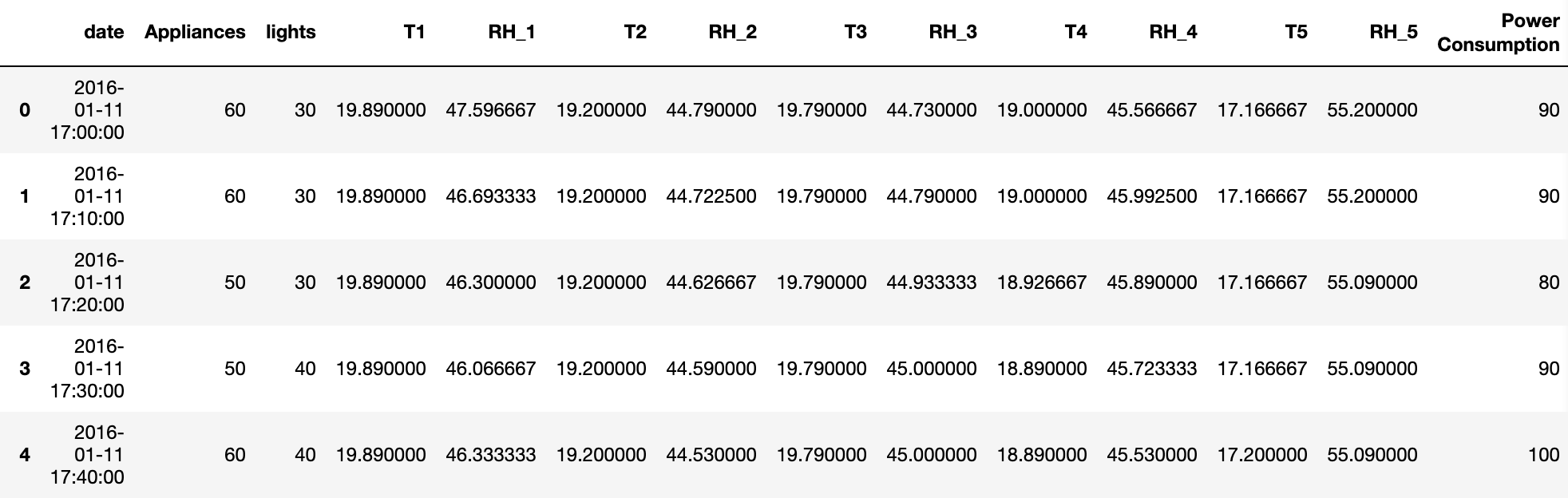
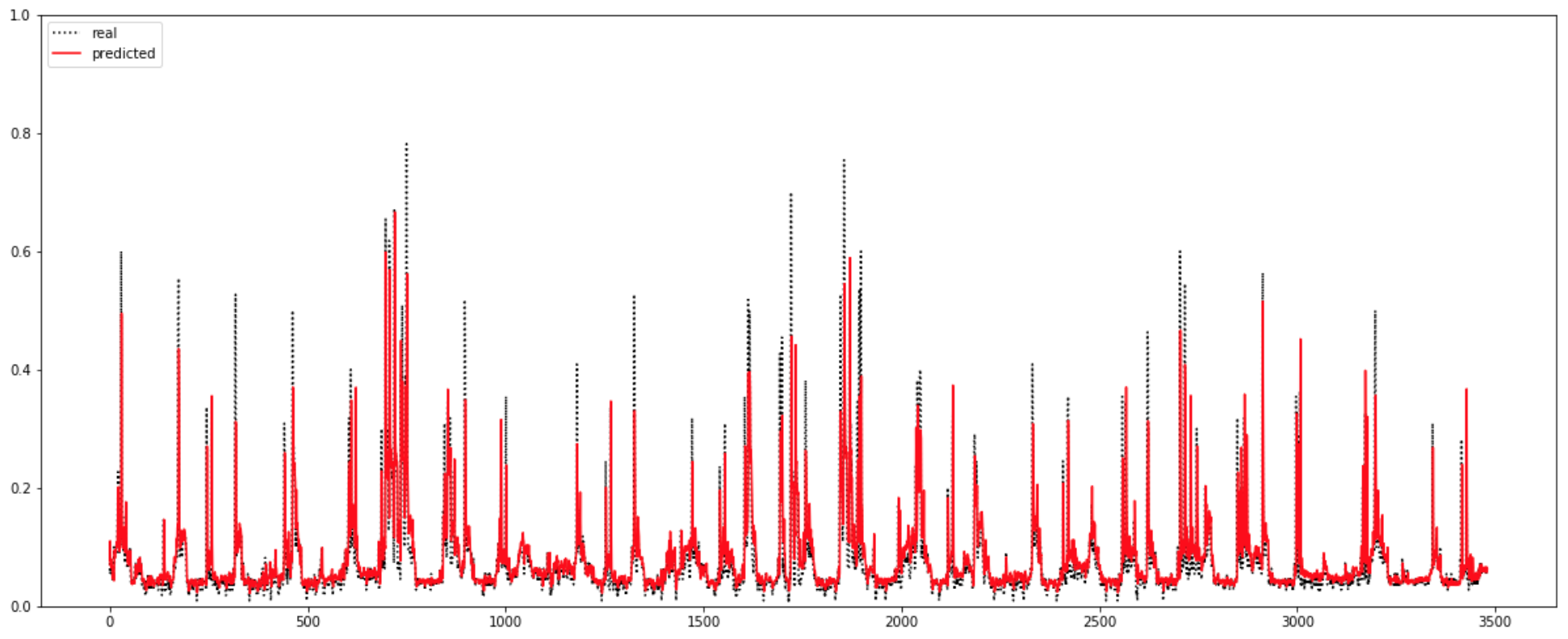
予測モデルは時系列データに強いと言われているLSTMを用いた。すると予測結果は図3のようになる。破線はデータ値で、赤線が予測値である。但し値は0から1になるように正規化されているため、正規化された赤線の値を元に戻した値が\(P_{ML}(t+\tau)\)である。図3を見て分かるように電力需要量が多い時の予測値は実際の値とかなりずれているが、それは想定内で、それ以外の時は良く予測されている。この予測値を波力発電装置の制御に用いる。
3. 並進動揺型の波力発電装置の制御
まず、波浪中を自由に動揺する浮体（水面に浮く物体の総称）の問題は船舶流体力学の知識から、以下の二つの問題に分別することができる。
ディフラクション問題において浮体に働く力には以下のようなものがある。但し、重力と浮力は釣り合っているとして除外する。
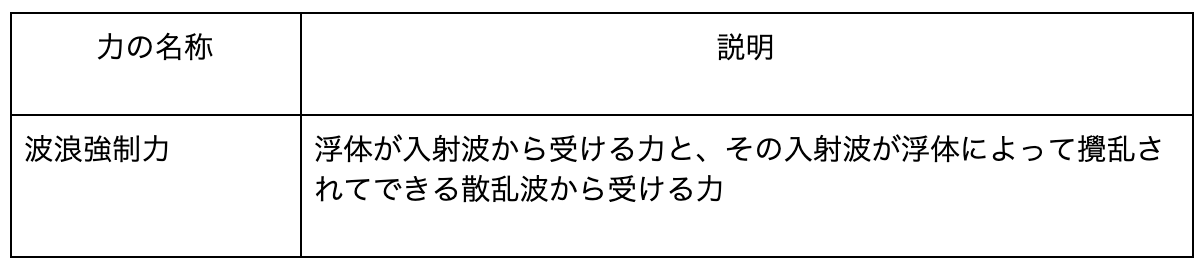
ラディエイション問題において浮体に働く力には以下のようなものがある。
まず浮体の動揺を制御していない場合、波浪中の浮体の運動方程式は、浮体の上下方向の運動変位を\(z\)、上記で示したラディエイション力、復原力、波浪強制力の上下方向成分をそれぞれ\(F_{3}^{R}(\ddot{z},\dot{z})\)、\(F_{3}^{S}(\ddot{z},\dot{z})\)、\(F_{3}^{W}(\ddot{z},\dot{z})\)とすると、 \[ m\ddot{z}(t)=F_{3}^{R}(\ddot{z},\dot{z})+F_{3}^{S}(z)+F_{3}^{W}(t)\tag{1} \] と表せる。ここで\(F_{3}^{R}(\ddot{z},\dot{z})\)、\(F_{3}^{S}(z)\)、\(F_{3}^{W}(t)\)は数値計算または計測されていて既知であるとする。
次に浮体の動揺を制御する場合、浮体の運動方程式は式に制御力\(G_{3}(t)\)を加えて、 \[ m\ddot{z}(t)=F_{3}^{R}(\ddot{z},\dot{z})+F_{3}^{S}(z)+F_{3}^{W}(t)+G_{3}(t)\tag{2} \] と表せる。この制御力\(G_{3}(t)\)を調節することで、望んでいる量を発電するように浮体を動揺させることができる。
発電量\(P(t)~[W]\)は、発電機構の巻線抵抗\(R_{s}~[\Omega]\)、推力係数\(K_{t}~[N/A]\)を用いると、機械入力\(-G_{3}(t)\dot{z}(t)\)から発電ロス\(\cfrac{ R_{s} }{ K_{t}^{2} }G_{3}^{2}(t)\)の差として表せるので、 \[ P(t)=-G_{3}(t)\dot{z}(t)-\cfrac{ R_{s} }{ K_{t}^{2} }G_{3}^{2}(t)\tag{3} \] となる。
この発電量\(P(t)\)を、機械学習（machine learning）で予測した時刻\(t+\tau\)の電力需要量\(P_{ML}(t+\tau)\)となるように制御したいので、 \[ P(t)=P_{ML}(t+\tau)\tag{4} \] とする。すると式\((3)\)は\(G_{3}(t)\)の二次方程式 \[ \cfrac{ R_{s} }{ K_{t}^{2} }G_{3}^{2}(t)+\dot{z}(t)G_{3}(t)+P_{ML}(t+\tau)=0\tag{5} \] となる。二次方程式の解の公式より、制御力\(G_{3}(t)\)は \[ G_{3}(t)=G_{3}(\dot{z})=\frac{ -\dot{z}(t)\pm\sqrt{ \dot{z}^2(t)-4\cfrac{ R_{s} }{ K_{t}^{2} }P_{ML}(t+\tau) } }{ 2\cfrac{ R_{s} }{ K_{t}^{2} }}\tag{6} \] と求まり、浮体の上下揺の速度\(\dot{z}\)の関数となる。この制御力\(G_{3}(\dot{z})\)を式\((2)\)に代入することで、浮体の動揺は\(P_{ML}(t+\tau)\)だけ発電するように制御される。
4. 考察
上記で示したように制御することで、確かに需要と供給のバランスを常に保ちながら発電することができる。ただ、今回は実装の手順を示すことを目的として電力需要量の予測の精度については気にしなかったが、本来はここが極めて重要である。2章でも示したが、今回使用したデータは1年に満たないデータ数である。これでは電力需要量の朝、昼、夜の変化は捉えることができたとしても、季節の変化は捉えることができない。これが予測精度を落としている明らかな理由である。
また、今回は10分間で送電が完了するという状況を考えたためそう遠くない未来の電力需要量を予測するだけであったが、実際波力発電装置が陸地からかなり遠い沖合に設置された場合、10分で送電できるとは考えられない。つまりもっと先の未来の電力需要量を予測できなければならない。実際に今回のデータセットで1時間先の電力需要量を予測してみたところ、かなり酷い精度になり、これでは波力発電装置の制御には使えないという結果となった。しかしこの原因もデータ数が足りないことであることは分かっている。季節の影響を捉えていないモデルで、未来を上手く予測できないのは当然である。
上記二つの問題はデータ数を増やすことで改善できるので、長い期間の電力需要量のデータを入手次第、改めてやり直そうと考えている。
問題はまだある。それは発電量が多い時、精度が悪くなることである。これは今のところ原因が分かっていないので、引き続き研究していく。
また、今回は求めている発電量を発電できるような制御を行ったが、安全性については全く考慮していない。たとえ電力需要量と同量発電できたとしても、事故を起こしてしまっては元も子もない。なので、今回の制御に安全性の配慮を加えた研究も今後行っていく。
5.参考文献
- 国土交通省「海洋開発工学概論 海洋再生可能エネルギー開発編 改訂第1版」, 2018（最終閲覧日2019年12月26日）
- 柏木正、岩下英嗣『船舶海洋工学シリーズ④ 船体運動 耐航性能編』公益財団法人 日本船舶海洋工学会, 2012
- 谷口友基、井上俊司、藤原敏文、大塚敏之「モデル予測制御による波力発電装置の高効率化」, 2019（最終閲覧日2019年12月26日）
Twitter・Facebookで定期的に情報発信しています！
Follow @acceluniverse
関連記事
目次 背景 原因究明 解決策 結果 背景 AUCでは、SRE活動の一環として、AWSコストの適正化を行っています。 （技術ブログ『SRE：コスト抑制のための異常値検知機構の実装』） コスト適正化における課題は、大きく分けて下記の4つです。 ①コストは月末にチェックしており、月中でコストが急激に上昇した場合発見が遅れてしまう。 ② 不要なリソースが放置されていたり、新たなリリースによって生じたコストを確認していない。 ③ AWSが提供するベスト
目次 実装前の課題 採用した技術と理由 実装した内容の紹介 改善したこと（抑制できたコスト） 実装前の課題 SRE（Site Reliability Engineering：サイト信頼性エンジニアリング）とは、Googleが提唱したシステム管理とサービス運用に対するアプローチです。システムの信頼性に焦点を置き、企業が保有する全てのシステムの管理、問題解決、運用タスクの自動化を行います。 弊社では2021年2月からSRE活動を行っており、セキュリ
目次 AUCの使用ツール GitHub、CircleCI使用までの流れ AWSの構成図 まとめ AUCの使用ツール 弊社ではGitHubとCircleCIの2つのツールを利用し、DevOpsの概念を実現しております。 DevOpsとは、開発者(Development)と運用者(Operations)が強調することで、ユーザーにとってより価値の高いシステムを提供する、という概念です。 開発者は、「システムへ新しい機能を追加したい」 運用者は、「システムを
2022年卒大学生の皆さん！ コロナウイルスが流行していることで就活にどういう影響があるのか、とても不安ですよね。 今回は業界ごとに採用人数を予測し、「どの業界が狙い目なのか」機械学習を使った分析手順を紹介します！ 目次 概要 手順 今後の課題 1.概要 データセットの内容 分析対象の7業界・各4企業 化粧品 電子機器 商社 不動産 金融 サービス IT・情報 説明変数と目的変数 特徴量 年初の株価、決算報告書提出翌日の株価、一株あたりの純資産額、従業員数