こんにちは、システム部の大瀧です。

今回は初歩ということでGoogle Colaboratoryを使ってみようと思います。
せっかくなので実際に動くものとして、scikit-learnが用意しているbostonのデータセットを使って初歩的な単回帰分析を行ってみます。

1. Google Colaboratoryとは

Colaboratoryは、完全にクラウドで実行されるJupyterノートブック環境です。設定不要で、無料でご利用になれます。
Colaboratoryを使用すると、コードの記述と実行、解析の保存や共有、強力なコンピューティングリソースへのアクセスなどをブラウザからすべて無料で行えます。

Google Codelaboratoryへようこそ より

つまりGoogle Colaboratory(以下Colab, コラボと読むようです)は、端的にいうとクラウド版のjupyter notebookということです。
誰でも無料で簡単に利用することができるという敷居の低さや、GPU環境を無料で利用可能であることなどがColabのメリットです。

補足. jupyter notebookとは

「jupyter notebookが何か」を簡潔にいうとプログラムの実行環境のことなのですが、優れているのはnotebookというだけあってコードだけでなくメモやファイル、コードの実行結果などをノートのように残すことができる点です。
特にデータの処理を行ったグラフなどを残しておけるのは非常に見やすく、データを分析する助けになります。

2. 実際に動かしてみる

Colabの準備は簡単です。
Googleアカウントを用意しましょう。それだけです。

https://colab.research.google.com/にアクセスします。
以下のような画面が表示されるはずです。

次に新しいノートブックを作成します。
メニューの「ファイル」から「Python3の新しいノートブック」を選択すると真っさらなノートブックが作成されます。

画像の赤枠が「セル」と呼ばれ、コードはセル単位で実行することが可能です。
せっかくなので簡単にコードを記載してみます。
今回はscikit-learnというライブラリのBostonデータセットを使ってなんちゃって線形回帰を試してみたいと思います。

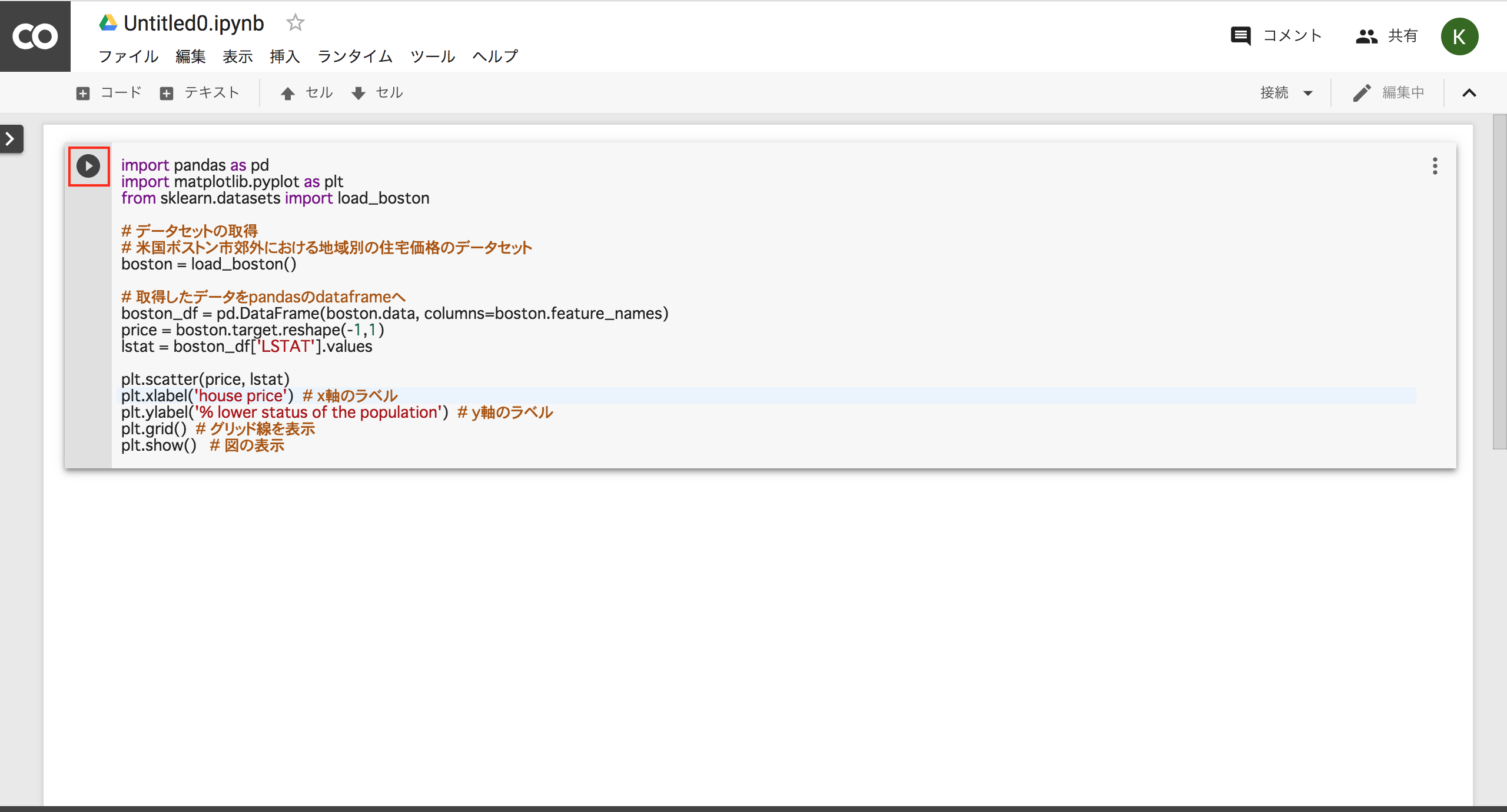
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston

# データセットの取得
# 米国ボストン市郊外における地域別の住宅価格のデータセット
boston = load_boston()

# 取得したデータをpandasのdataframeへ
boston_df = pd.DataFrame(boston.data, columns=boston.feature_names)
price = boston.target.reshape(-1,1)
lstat = boston_df['LSTAT'].values
plt.scatter(price, lstat)
plt.xlabel('house price') # x軸のラベル
plt.ylabel('% lower status of the population') # y軸のラベル
plt.grid() # グリッド線を表示
plt.show() # 図の表示

実行するコードをセルに書き込んだらセルの左上にある再生ボタン?を押しましょう。これでコードが実行されます。
もし複数のセルを実行したい場合は、メニューにある「ランタイム」の項目の「すべてのセルを実行」を選択してください。他にも一部のセルのみを実行することなどが可能です。

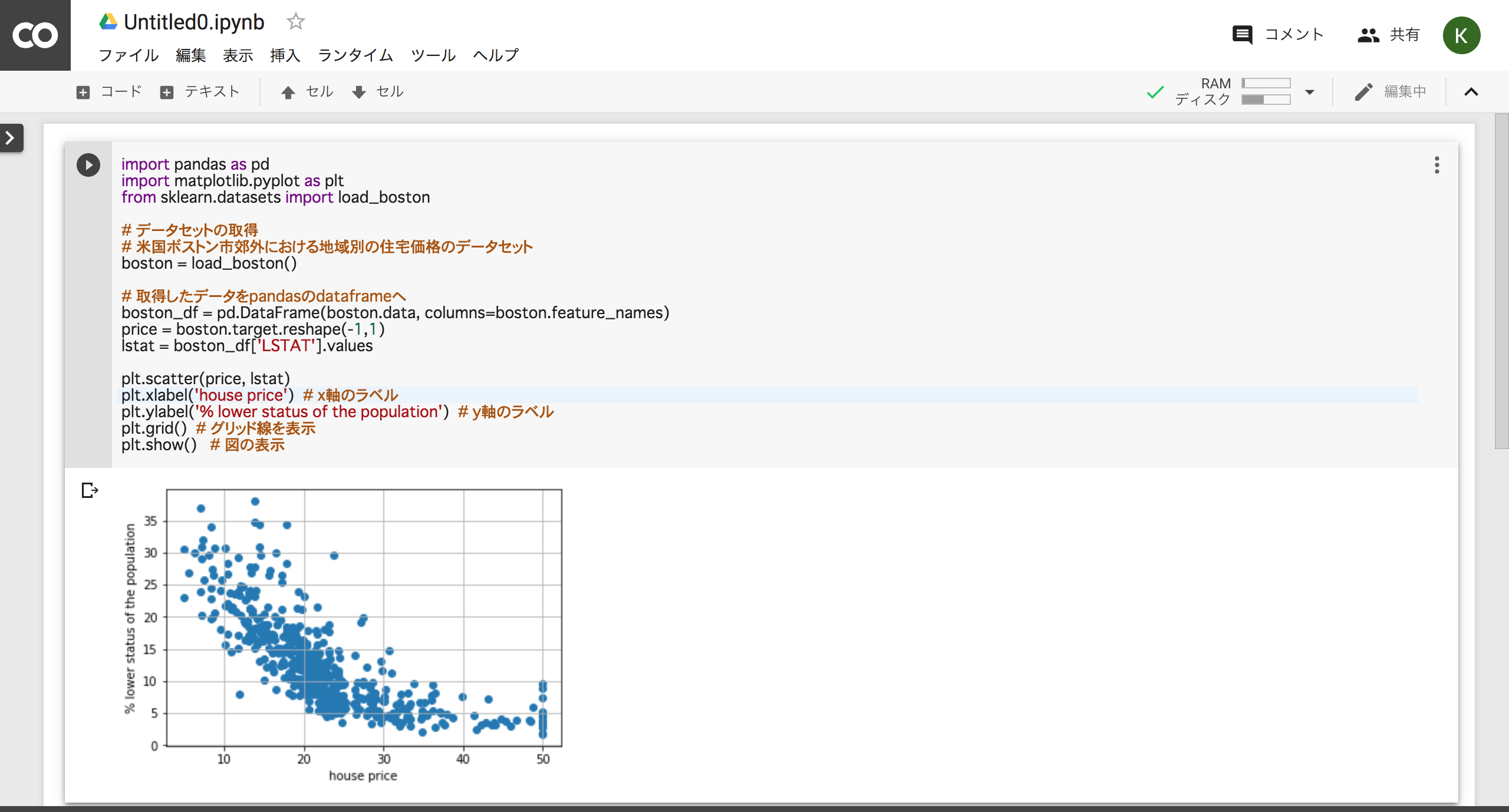
実行するとグラフが描画されます。
今回は「地域別住宅価格(X軸)」と「給与の低い職業に従事する人口の割合 (%)(Y軸)」のグラフです。プロットされたドットをみるとどうやら相関関係がありそうです。
当たり前かもしれませんが、住宅の価格が高い地域には給与の低い職業に従事する人が少ないようです。

ではこれらを線形回帰(今回は手抜き単回帰分析)します。
描画されたグラフはそのままに新たに分析結果を追加したグラフを描画します。
メニュー下の「＋コード」を押します。

新たに作成されたセルに新たにコードを書き込み、今回書き込んだセルの左上にある再生ボタンをクリックすると、このセルのみが実行されます。
画像のように線形直線が描画された新たなグラフが表示されたでしょうか。

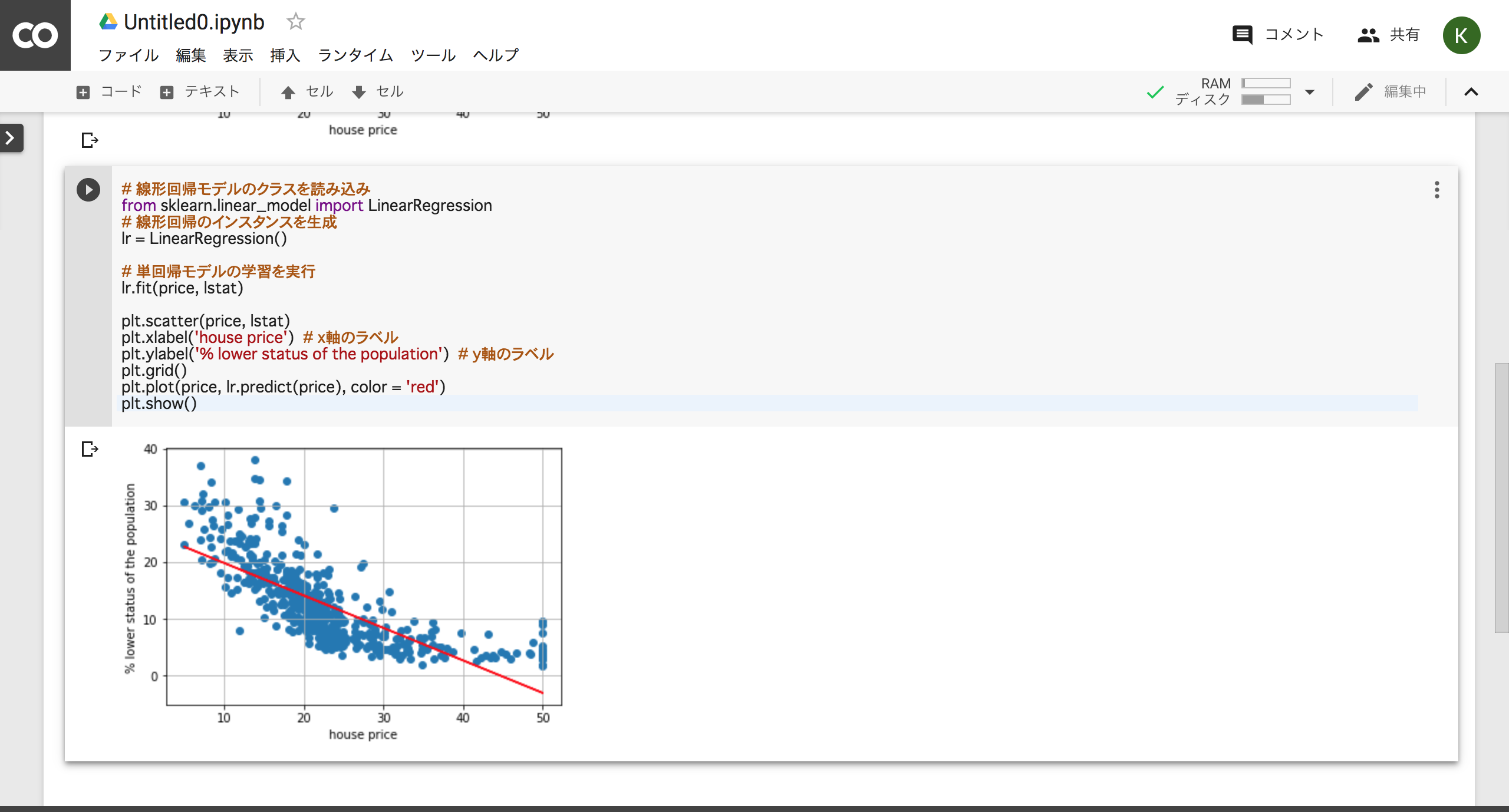
# 線形回帰モデルのクラスを読み込み
from sklearn.linear_model import LinearRegression
# 線形回帰のインスタンスを生成
lr = LinearRegression()

# 単回帰モデルの学習を実行
lr.fit(price, lstat)
plt.scatter(price, lstat)
plt.xlabel('house price') # x軸のラベル
plt.ylabel('% lower status of the population') # y軸のラベル
plt.grid()
plt.plot(price, lr.predict(price), color = 'red')
plt.show()

作成したファイルなのですが、アカウントのGoogle Drive内にColab Notebooksというフォルダができており、そこに保存されています。ここで察しがつくのですが、Google Driveに保存されているファイル(例えば集計データなど)をロードして、コードの中で使うことも容易になっており、そういう点もColabの魅了ですね。

今回のサンプルを公開しておきます[リンク]。
このように簡単に公開できることも大きな魅力ですが、これらを自身のワークスペースに複製して編集することなどもできます。

今回のサンプルはグラフの描画などを行いましたが、単純にPythonを初めて触る際にも使い勝手が良いかと思いますので是非使ってみましょう。