機械学習では、訓練データとテストデータの違いによって、一部のテストデータに対する精度が上がらないことがあります。

例えば、水辺の鳥と野原の鳥を分類するCUB(Caltech-UCSD Birds-200-2011)データセットに対する画像認識の問題が挙げられます。意図的にではありますが訓練データを、

• 水辺の鳥が写っている画像は背景が水辺のものが90％、野原のものが10％
• 野原の鳥が写っている画像は背景が水辺のものが10％、野原のものが90％

となるように分割します。このときに、訓練データの中で「背景が野原で水辺の鳥」の画像や「背景が水辺で野原の鳥」の画像が少なく、同じようなテストデータに対して精度が上がらないことがあります。

以降では、テストデータ全体の精度をaverage accuracyと呼ぶのに対して、このようなデータに対する精度をrobust accuracyと呼ぶことにします。パラメータの数が訓練データの数よりも多い(overparameterized)ニューラルネットワークでは、モデルの複雑度が高いために過学習しやすく、average accuracyは高くともrobust accuracyは低くなりがちです。

論文"Distributionally Robust Neural Networks"では、上記のような訓練データとテストデータの分布が異なるときのrobust accuracyを上げる最適化手法について説明されています。パラメータの多いニューラルネットワークがよく使われる画像認識や自然言語処理などのタスクに対して同じような最適化手法を適用でき、今後も広く使われる手法かもしれません。

この記事では論文で説明されていた手法について、簡単に概要を説明しようと思います。

"distributionally robust optimization"とは？

訓練データよりも多くパラメータが存在するニューラルネットワークでは、学習データにおけるロスの消失による過学習が問題となっていました。そのようなときは一般には平均的に汎化誤差(generalization gap)が小さくなるように最適化するのですが、どうしてもロスが最も大きいworst-case groupに対しては、依然汎化誤差大きいままになってしまいます。

そこで考えられた手法がdistributionally robust optimization(以下DRO)です。DROは一言で言えば最も大きいロスでの最小化です。

\[ \min_{\theta \in \Theta} \sup_{Q \in \mathcal{Q}} {\rm E}_{(x,y)\sim Q}[l(\theta;(x,y))] \]

\( \sup {\rm E}[l(\theta;(x,y))]\)が表すのがworst-case groupの平均のロスとなります。\(Q\)が表すのが分類する各グループ\(g\)ごとの分布の線形結合となるのですが、最小化は線形計画法のアルゴリズム(単体法)で行われます。そのため、最適解は実行可能領域の頂点、すなわちworst-case groupのみの分布における最適解と一致します。

\[ \min_{\theta \in \Theta} \max_{g \in \mathcal{G}} {\rm E}_{(x,y)\sim P_{g}}[l(\theta;(x,y))] \]

worst-case groupの分布では平均のロスが最も大きくなります。DROはその分布でのロスの最小化を目的とするアルゴリズムだと言えます。これまでの機械学習は平均的な汎化誤差を正則化(regularization)などによって低減させていましたが、DROはworst-case groupの精度の向上、つまりrobust accuracyの向上が目的です。

では、実際にどのようにしてworst-case groupの精度を向上させているのでしょうか？次節からはその具体的な手法について説明します。

従来手法によるrobust accuracyの向上

DROで使われる正則化の1つとして重み減衰(weight decay)が挙げられます。すでに様々な機械学習の中で使われている手法であり、例えば有名なものではL2正則化が挙げられます。

\[ E(w) + \cfrac{\lambda ||w||^{2}_{2}}{2} \]

論文では、画像認識のモデルであるResNet50においてL2正則化をするとき、\(\lambda\)は通常小さな値\((\lambda=0.0001)\)が設定されるが、この値を大きくするとrobust accuracyが上がるということが述べられています。つまり、強い重み減衰(strong weight decay)が手法の1つとして考えられます。

また、もう1つの正則化としてearly stoppingが挙げられます。こちらも機械学習でよく使われる手法ですが、想定されるニューラルネットワークのパラメータ数が多く学習数が大きいとすぐに過学習するため、early stoppingが有効だと言えます。

検証

それではDROの検証結果について見てみましょう。ベンチマークとしてERMモデルとの比較を行います。最初に述べたCUBのWaterbirdsの分類タスク(ResNet50による)の他に、CelebAデータセットにおける髪色の分類タスク(ResNet50による)と、MultiNLIデータセットにおける自然言語推論タスク(BERTによる)で比較しています。一般的な正則化(Standard Regularization)と前節で述べた2つの手法を試したときのaverage accuracy、robust accuracyは以下のとおりです。

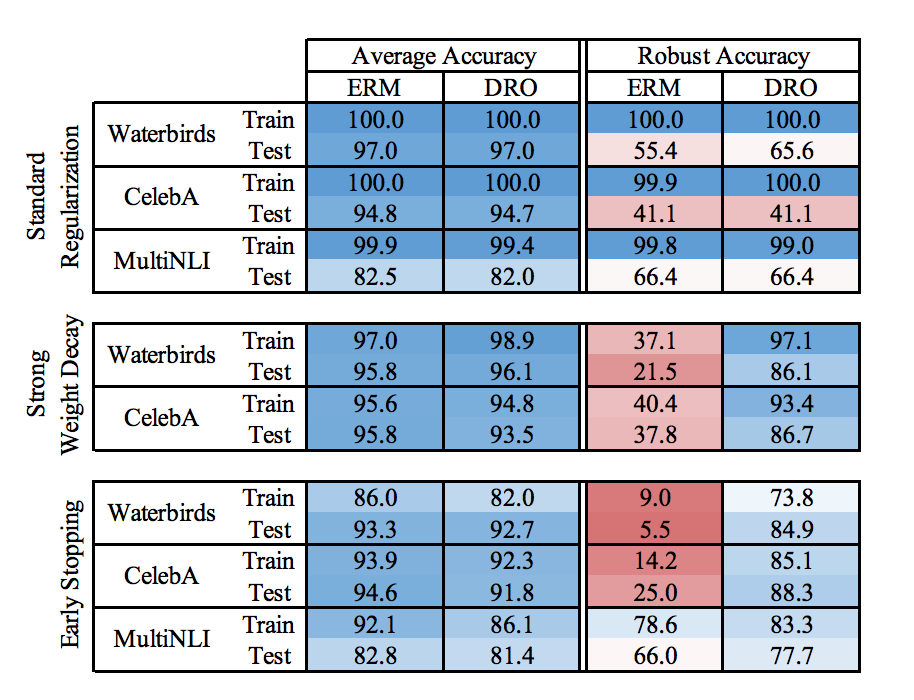
この結果からどのタスクにおいても、ERMではaverage accuracyに比べてrobust accuracyが大幅に低下したのに対して、DROのstrong weight decayとearly stoppingによってrobust accuracyが大幅に低下するのを防いでいることが確認できると思います。

また、CelebAに関してaccuracyの収束性についても見てみましょう。

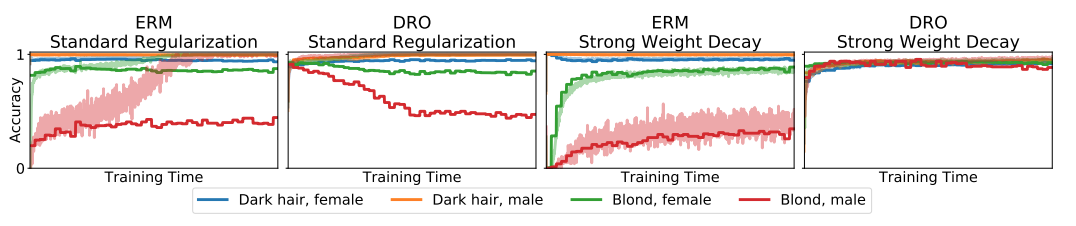
worst-case groupである「Blondの髪で性別がmale」の判別において、strong weight decayを用いたDROがそれぞれのグループで他の手法よりも良い収束性を持つことが確認できます。

グループサイズを利用した正則化

今回の論文では分類するグループの大きさを利用したDRO(group-adjusted DRO)についても述べられています。グループ内のデータの数を\(n_{g}\)とすると、最適化するべき目的関数は、

\[ \min_{\theta \in \Theta} \max_{g \in \mathcal{G}} {\rm E}_{(x,y)\sim P_{g}}[l(\theta;(x,y))] + \cfrac{C}{\sqrt{n_{g}}} \]

となります。ハイパーパラメータ\(C\)を用いた正則化項を付け加えるアイディアです。\(n_{g}\)の平方根の逆数を掛けることで、グループごとのデータ数を考慮した汎化をおこなうことができるようです。このgroup-adjusted DROのaccuracyは以下のようになっています。

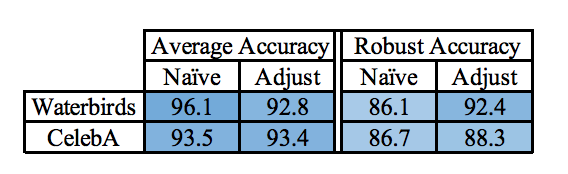
robust accuracyにおいてさらなる改善が見られますね。バリデーションによって\(C\)の値さえうまく決めることができればかなり役に立つ手法だと言えます。

importance weightingとの比較

実は同じような解決策として、importance weightingという従来手法が存在します。これはロスに重み付けした上で最小化を行う手法です。これはミニバッチからデータを等確率でリサンプリング(RS)することでrobust accuracyを上げる手法だそうです。こちらについてもベンチマークを見てみましょう。

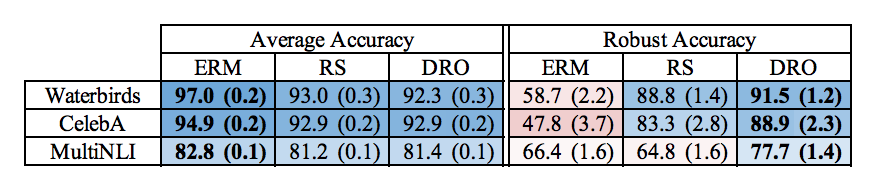
ERMよりもrobust accuracyが上がっていますが、DROほどではありません。DROは従来手法よりもrobust accuracyの向上に有効だと言えます。

終わりに

今回紹介した論文では訓練データとテストデータの分布の違いを考慮した手法であるDROについて簡単に紹介しました。従来よりもrobust accuracyを大きく上げたという点でより注目される手法だと思います。

しかし、なぜこのように正則化をすると精度が向上するのかという問いに対する明確な答えがまだない状態です。この論文を足がかりにrobust accuracyが上がる数理的なメカニズムが解明されれば、様々なモデルで汎化性能の向上が期待できるでしょう。

参考文献

DISTRIBUTIONALLY ROBUST NEURAL NETWORKS