はじめに

多くの機械学習モデルにおいて注意することの一つとして過学習(overfitting)があります。過学習は学習データに適合しすぎて未知のデータに適合できずに、汎化性能が低下してしまう現象のことを指します。DNNを例に取ると、モデルサイズを大きくしたり、エポック(epoch)及びイテレーション(iteration)を大きくしすぎるとモデルが過学習しすぎてテストエラー(汎化誤差)が大きくなってしまいます。ですが最近になって、一定以上を超えて上記のパラメータを大きくしていくとテストエラーが減少する"Double Descent"という現象が報告されているようです。今回はこの現象が起きている要因を解析している論文"Deep Double Descent: Where Bigger Models and More Data Hurt"の要約をしていこうと思います。

"Double Descent"とは

[The Elements of Statistical Learning]
この文献で述べられているように、従来ではモデルの複雑度(complexity)がある閾値を超えるとテストエラーが大きくなり続けるということが言われていました。一方で、ここ最近では100万を超えるパラメータを持つ巨大なモデルを構築する、学習回数を増やす、データを増やすことでテストエラーが改善していくという論文がここ5年の間に次々と報告されてきています。以下の図のように一度降下して再度降下していく現象を"Double Descent"と名付けられています。

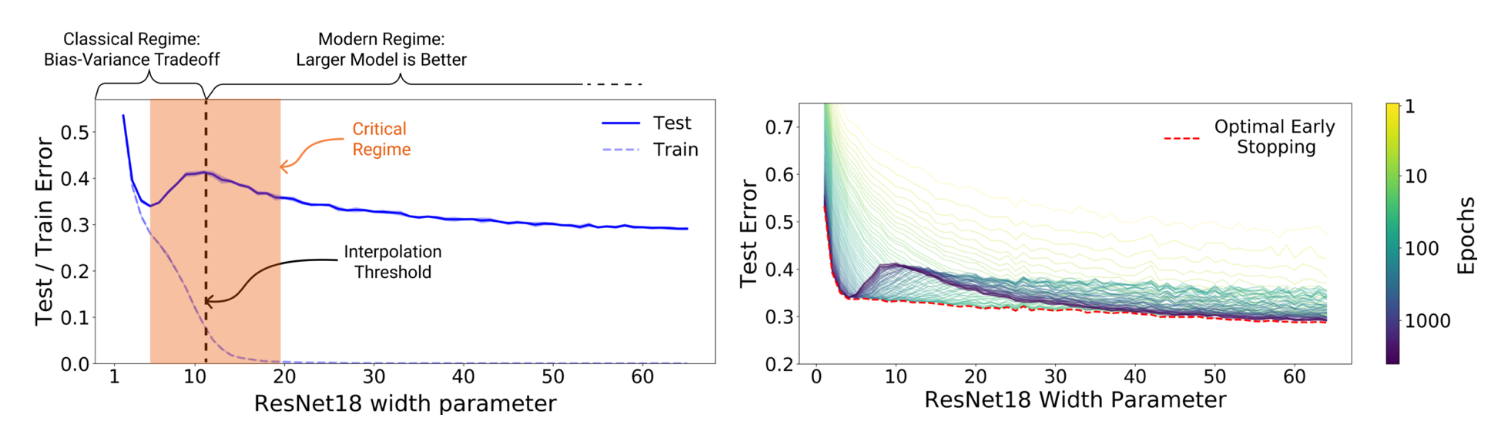
このグラフの特性は2つの領域に大別できます。上記で述べたテストエラーが悪くなり続けるという話は" Classical regime"のことを示しており、複雑度(モデルの構造や学習量)を一定以上に大きくすると再度降下していく"Modern regime"がその後に続いています。例えばシンプルな構造のニューラルネットワークと複雑なニューラルネットワークがあったとします。前者については従来から言われているように"under-fitting"と"over-fitting"からなるU字型の特性が観測できますが、後者は複雑にしていくとある閾値（図でいうinterpolation threshhold）で再度降下していくという具合です。
さて"Double Descent"についてはなんとなくわかりましたが、どのような要因によってこのような特性となるのでしょうか。次に論文の主軸であるEMCという指標について述べていきます。

EMCについて

EMCとは"トレーニングエラーがほぼ0になるときのサンプルの最大値"で定義されています。もちろんですがtraining errorが0になる時点というのは使用するモデルや学習方法や量、問題によって異なってきます。筆者はこのEMCという指標でDouble Descentを説明できるという仮設を立てています。
上記の文を式にすると以下のようになります。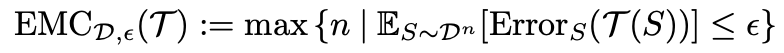
ただし、
S:入力データ
D:データの分布
T:学習手順
n:サンプル数
ε:トレーニングエラー

上記の定義式を元に以下の図のように3つの領域に分けられます。

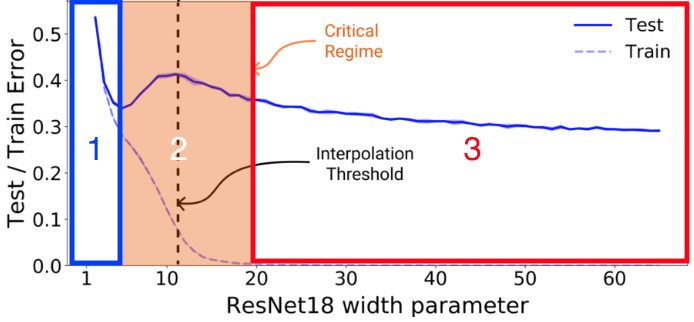
1. Uner-parameterized regime

EMCが大幅にnより小さいとき、複雑度が増加すると同時にテストエラーは減少する（EMC<n）

2. Critically parameterized regime

EMCがnにほぼ等しいとき、複雑度が増加すると同時にテストエラーは減少する若しくは増加する（EMC>n）

3. Over-parameterized regime

EMCが大幅にnより大きいとき、複雑度が増加すると同時にテストエラーは減少する（EMC≒n）

まだ分かりづらいと思うので補足します。横軸をsample数としてCritically parameterized regimeの部分に注目したグラフが以下のようになっています。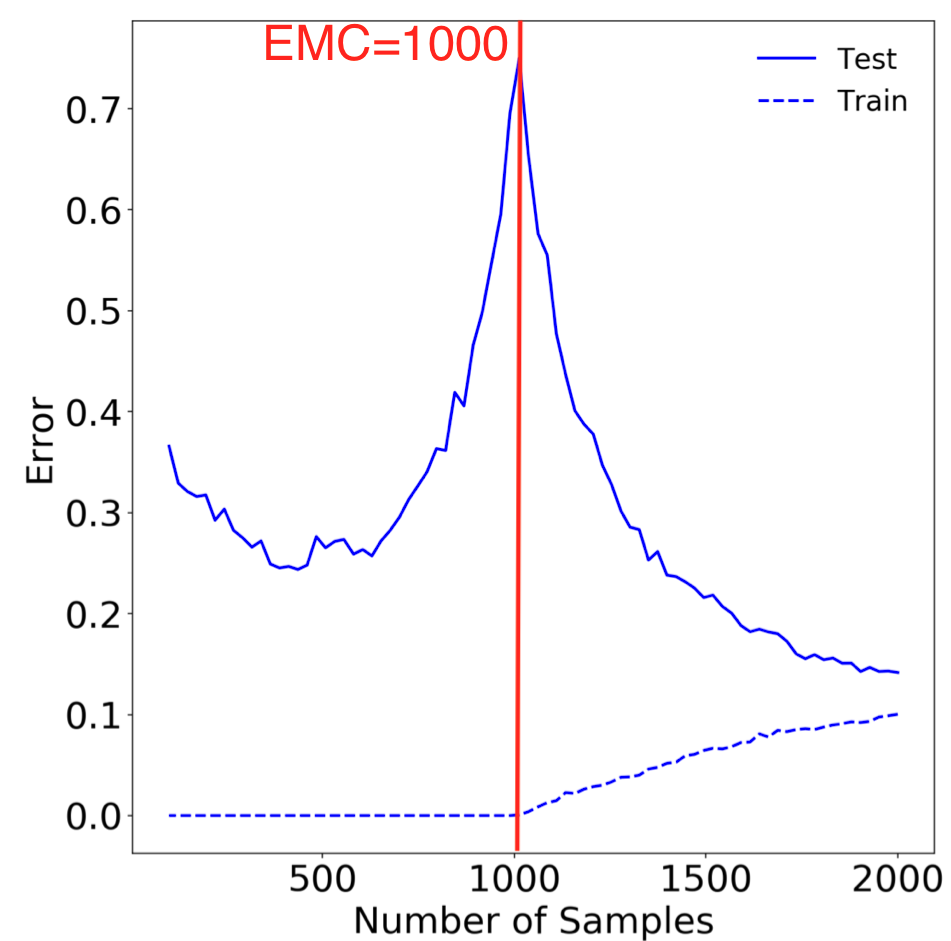

定義通り捉えるとトレーニングエラーεが0付近の中でもサンプル数が最大となるのはおよそ1000となっているのでEMCは1000となります。この場合ではテストエラーのグラフのinterpolation threshholdはこの値付近に存在するということになります。もちろんこのグラフ特性は入力データSと分布D、学習手順T（これはモデルサイズは最適化アルゴリズムを含む）によって変化します。が、それぞれのパターン毎において求められるEMCの値付近にこのinterpolation threshholdが「経験則的に」存在している、つまりEMCとinterpolation threshholdは何かしらの相関が存在しているため、その延長線上に有るDouble DescentはEMCによって説明出来るという仮説が本論文の趣旨です。

　あくまでも仮説なので、EMC=nとなる付近でinterpolation threshholdが存在するということを以下の理論解析で説明しています。また、εの値は経験則的に決められており（ε= 0.1）、原則が存在するわけではないようです。図から分かるようにCritically parameterized regimeでは過学習のような振る舞いをしているため、汎化性能が劣化している領域です。そのため、予めこの領域を把握していれば汎化性能の劣化を防ぐことが出来るということですね。ということで以降はEMCに相関のあるモデルサイズ、学習量等を評価軸としてDouble Descentの振る舞いを見ていきます。

その前に

理論解析で採用されているLabel Noiseについて説明します。これは教師データの正解ラベルをpの割合で誤った正解ラベルに置き換えることでデータ分布を強制的に変えている雑音のことを指します。（以下イメージ図）Label Noiseを付加することでモデルが誤って学習をすすめるため、過学習のような特性になることが予想できます。また、εが非常に小さくなるまで学習をすすめることで テストエラーの理論限界はpになることも予想できます。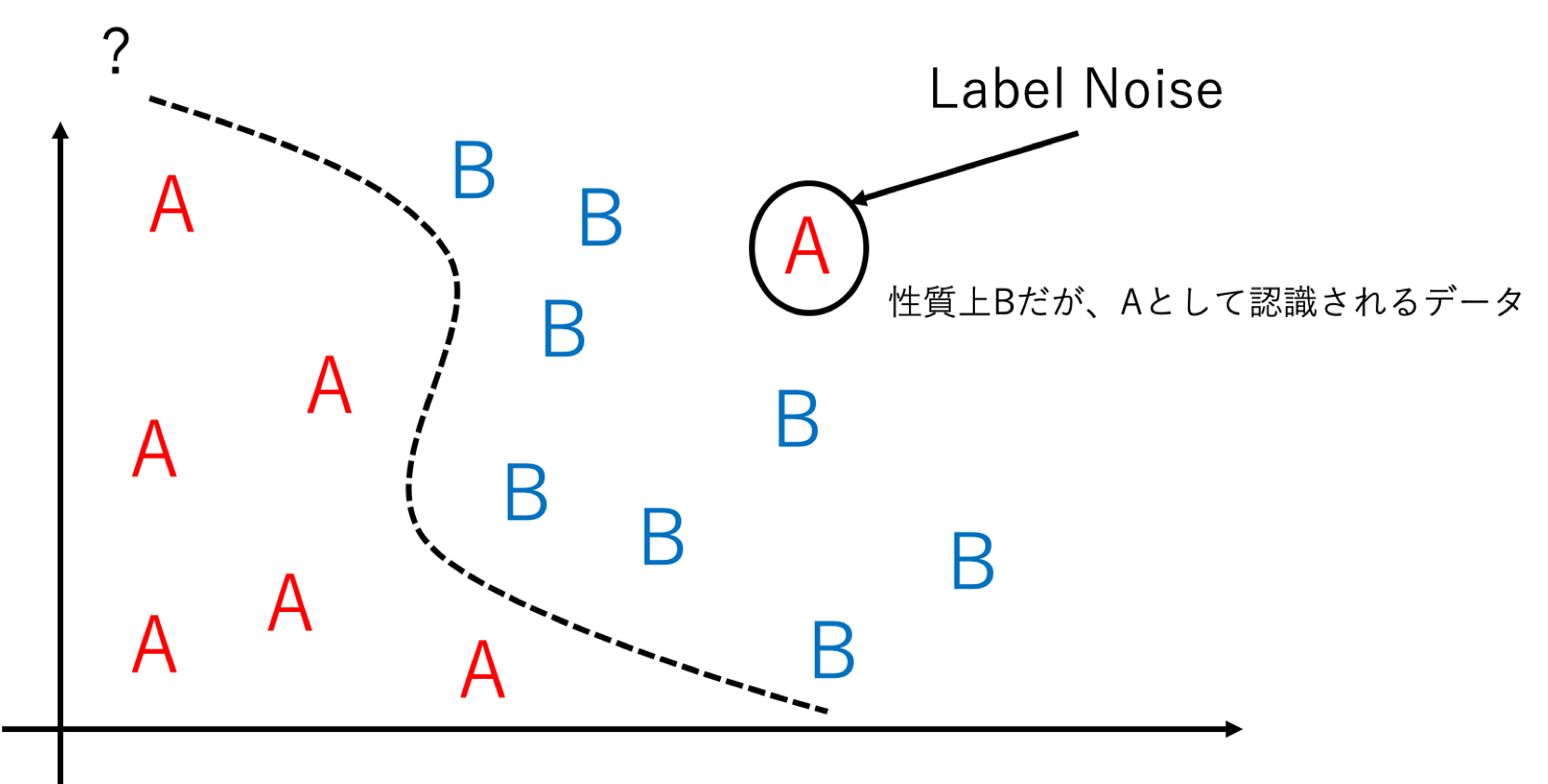

それでは各種評価について見ていきます。今回評価軸は3つに大別できます。

・Model-wise Double Descentーモデル構造（モデルサイズ、最適化アルゴリズム）の変更やデータの水増しによるDouble Descentの特性（エポック固定）
・Epoch-wise Double Descentーいわゆる学習曲線（モデル構造固定）
・Sample-wise Non monotonicityーサンプル数変化によるDouble Descentの振る舞い及びCritically parameterized regime付近での特性

それぞれ多角的に評価しており、その一部を記載していきます。

1.Model-wise Double Descent

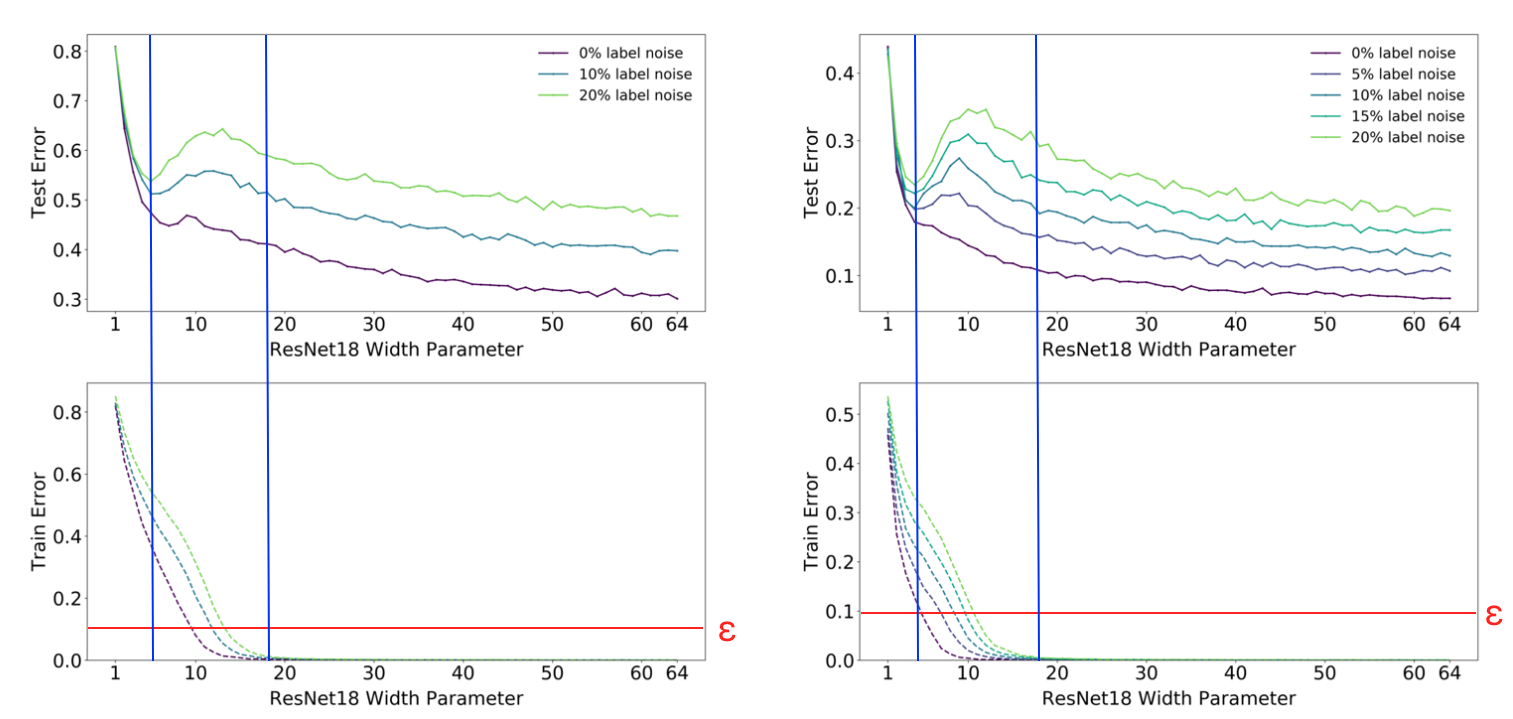○諸元
モデル：ResNet18
最適化アルゴリズム：Adam（learning rate:0.0001）
エポック数：4000
その他：データ水増し
データセット:左 CIFAR-100、右 CIFAR-10
上記はモデルサイズ毎のテストエラー、トレーニングエラーの特性を示しています。両者グラフの違いとして左の結果はLabel Noiseを付加していない場合でも"Double Descent"のような振る舞いをしていることがわかります。また、Label Noiseが大きくなるにつれてinterpolation threshholdにおけるピーク値が大きくなり、左にシフトしていっていることも読み取れます。

2.Epoch-wise Double Descent

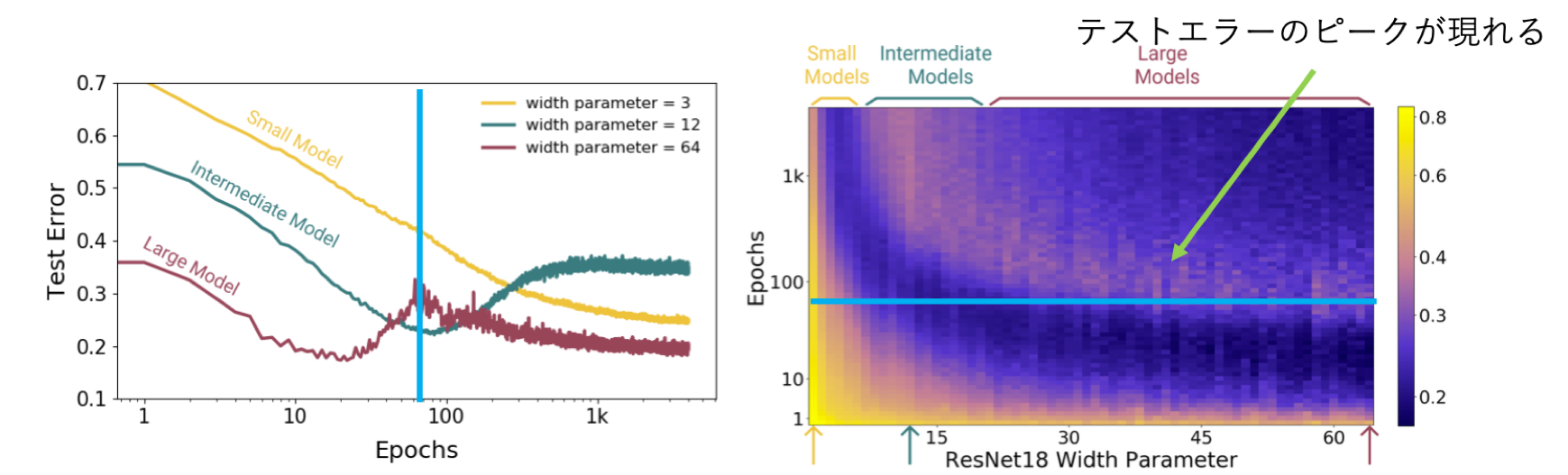
○諸元
モデル：ResNet18
最適化アルゴリズム：Adam（learning rate:0.0001）
Label Noise：20%
その他：データ水増し
データセット：CIFAR-10
次に学習量に応じたテストエラーを見ていきます。左のグラフが馴染みのある学習曲線、右はテストエラーを深さとしたデプスマッピングです。学習量が多くなるにつれてEMCが大きくなることから、モデルサイズが大きくなるにつれてDouble Descentのような振る舞いが顕著に現れていることがわかります。また他のサイズでは範囲内の学習量ではUner-parameterized regimeの領域に属していることからモデルが小さい場合は引き続き学習を続け、その間のサイズであれば早期終了するなどして学習を止めたほうが良い事が読み取れます。

3.Sample-wise Non monotonicity

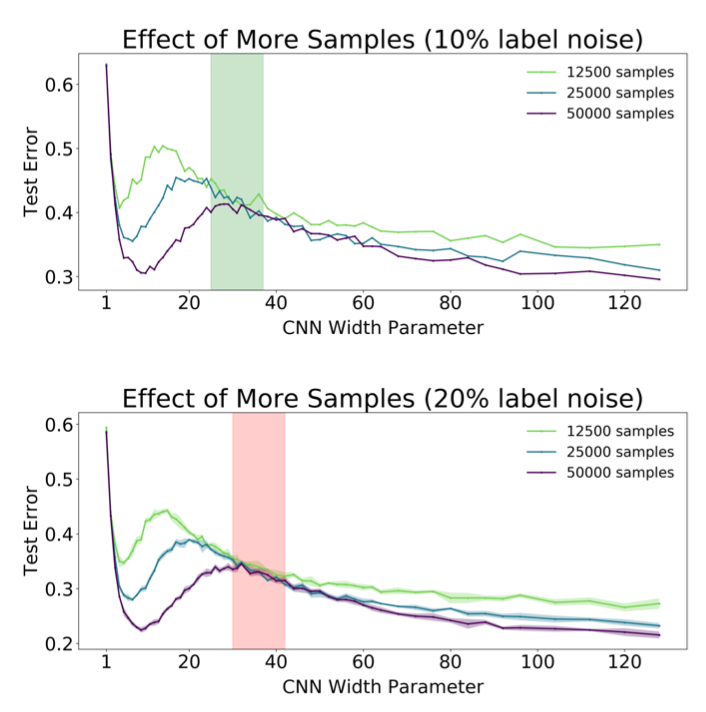
○諸元
モデル：5-layers CNN
最適化アルゴリズム：SGD（learning rate:0.0001）
データセット：CIFAR-10
最後にサンプル数変化によるDouble Descentの振る舞いを見ていきます。サンプル数を増やすことでEMCが増加するため、interpolation threshholdが右にシフトします。そのため、モデル固定の場合にCritically parameterized regimeをサンプル数によって調整出来るため、汎化性能が劣化することを予め回避することができます。（例えばoverfitting に位置するモデルのサンプル数を増やすことでunderfittingの位置にシフト出来る）個人的に気になったのですが、Label Noiseが小さい上のグラフのほうがテストエラーが大きくなっているのが疑問に思いました。

結果まとめ

終わりに

Fully understanding the mechanisms behind model-wise double descent in deep neu- ral networks remains an important open question. However, an analog of model-wise double descent occurs even for linear models. A recent stream of theoretical works analyzes this setting (Bartlett et al. (2019); Muthukumar et al. (2019); Belkin et al. (2019); Mei & Montanari (2019); Hastie et al. (2019)). We believe similar mechanisms may be at work in deep neural networks.

今回、"Double Descent"をEMCという指標で説明出来るという仮説を立てた事、またその根拠を理論解析で提示した論文の紹介をしました。上記の引用からも論理的な証明はまだできておらず発展途上ということだそうです。この"Double Descent"を解明することで、どれくらいの学習をさせるべきなのか事前に把握することができると同時に、モデルチューニングの最適化などにも貢献する重要なテーマであると思いました。

参考文献
・Trevor Hastie, Robert Tibshirani, Jerome Friedman"The Elements of Statistical Learning Data Mining, Inference, and Prediction,"Available:https://openreview.net/forum?id=B1g5sA4twr
・Preetum Nakkiran, Gal Kaplun, Yamini Bansal, Tristan Yang, Boaz Barak, Ilya Sutskever "DEEP DOUBLE DESCENT: WHERE BIGGER MODELS AND MORE DATA HURT," ICLR 2020 Conference Blind Submission, Available:https://openreview.net/attachment?id=B1g5sA4twr&name=original_pdf

Twitter・Facebookで定期的に情報発信しています！
Follow @acceluniverse