"TASK2VEC"は2019年2月にsubmitされた論文の中で提唱された手法であり、「タスクをベクトル化する」手法です。 この手法が提唱されるまでは、"タスク間の関係を表現する"フレームワークが存在しなかったため、一部界隈で脚光を浴びました。
しかし、このTASK2VECの言わんとすることが理解出来ても、どういうものなのか正直ちょっとわかりにくいです。そこで今回は出来るだけ論文の内容をかみ砕いて解説したいと思います。

目次

1.TASK2VEC 概要
2.事前知識
3.TASK2VEC 手順
4.論文の実験結果
5.まとめ
6.参考文献

1.TASK2VEC 概要

上でも述べたように、"TASK2VEC"は「タスク」または対応するデータセットをベクトル化します。ここで言う「タスク」とはデータセットとラベルの組み合わせのことです。
この論文によると、事前学習によって得られたモデルを利用し、タスクの埋め込み表現、つまりベクトル表現を獲得します。 これによってタスクの間の類似度を算出でき、適切な事前学習済みモデルを選択できるようになるということです。
例えば、「犬」の画像認識を行うことを考える時、「人」の画像認識で用いたパラメータより「猫」の画像認識で用いたパラメータを使って画像分類した方が良さそうですよね。直感的にはこういうことです。

さらに具体的に見ていきましょう。ここでは次の節の事前知識を見ておくと良いです(特にFIMのところ)。
本論文では「probe network」と呼ばれるネットワーク(特徴抽出器)を用います。 この「probe network」はImageNetで事前学習させた唯一の特徴抽出器であり、この事前学習ののち、特定のタスクの分類レイヤでのみ再学習させます。 学習が完了したら、特徴抽出器で得られたパラメータのFIMを計算します。このFIMはタスクに関する重要な情報を含んでいるのですが、これについては後述します。
ここでは「probe network」という単一の特徴抽出器を用いているため、各タスクを固定長の、つまりクラス数などの詳細に依存しないベクトルとして埋め込むことができるということです。

活用事例

このTASK2VECですが、実際に社会に活用できることとして考えられるのが、

画像を分類したい→データ数が少ないので転移学習を使おう
→良い学習済みモデルないかな？TASK2VECで探してみよう！

などの一連の流れが考えられます。ちょっと抽象的かもしれませんが、つまりはサンプル数が少なすぎても諦めないで！という感じです。 (強化学習の考え方に近いかもしれません)

2.事前知識

転移学習(Transfer Learning)

この記事をご覧になっている方は、この「転移学習」について既にご存知かと思いますが簡単に説明します。 転移学習とは、ある領域(ドメイン)で学習させたことを、他の領域に役立たせ効率よく学習させることです。事前に学習させたモデルを学習済みモデルと言ったりします。 「データの時代」と言われるこの世の中ですが、データの入手が困難なケースもあります。そういった少ないデータ量で学習を進めていく際、この転移学習は真価を発揮します。 また数万〜数十万もの教師データを集め、各々にラベル付けを行うにはかなりの人件コストがかかります。このように、既にある(精度のいい)モデルを、別のものに使いまわす転移学習はこれからの時代必要不可欠でしょう。

転移学習のステップとして、
1.与えられたデータから、特徴量を抽出:
学習済みモデルの最終層以外の部分を利用して、データ内の特徴量を抽出します。ここで得られた学習済みモデルを「特徴抽出器」と言います。

2.抽出した特徴量を用いて、クラス分類する:
1.で実際に求めた特徴量を用いて、新しく追加したモデルに学習を施します。特に画像や音声を識別するモデルは他の分野に比べて流用しやすいため、転移学習が役立ちます。

この転移学習の可能性について、かの有名なcourseraの講師であるAndrew Ngは「機械学習の成功を今後推進するのは、教師なし学習、そして最近目覚ましい進化を遂げている強化学習でもなく、転移学習である」と言及しています。

メタ学習(Meta Learning)

メタ学習とは、「学習方法を学習する(learning to learn)」ことに他なりません。
人間で例えるなら、勉強をする際に教科書や参考書を読み込んだりしますが、ただ読むとしてもその方法は人によって様々です。 そこで、効率が良く理解しやすい読み方が分かれば勉強しやすいですよね。その方法を学習するのがここで言うメタ学習です。

ディープラーニングにおけるメタ学習は次の3つのステップに分けられます。

1.どのタスクでも、同じディープラーニングモデルを使う
2. 各タスク自体がどのようなものかを表す特徴ベクトルをディープラーニングによって抽出し、このベクトルと1.のモデルを使ってタスクを行う
3.各タスクで少数のデータを使って再学習させ、満遍なく良い結果が得られる1.のモデルを見つける

結果として、様々なタスクに特化したモデルが得られると言うわけです。

フィッシャー情報行列(FIM)

タスクを解くためには、入力\(x\)とそれに対応するラベル\(y\)の関係\(p_w (y|x)\)を学習する必要があります。 \(p_w (y|x)\)は重み\(w\)において入力\(x\)(例えば画像データ)が与えられた時、クラス(ラベル)が\(y\)である確率を示しています。
ここで、パラメータ\(w\)がこのタスクを解く際にどれほど重要な情報を含んでいるのか知るために、その摂動\(w'=w+\delta w\)について考えます。 \(p_w (y|x)\)と\(p_{w'} (y|x)\)が大きく異なるようであれば、そのタスクはパラメータに大きく依存していることがわかります。
これを計算する指標としてKLダイバージェンスと呼ばれるものがあります。その二次近似は、 \(\hat{p}\)を訓練データによって定義される経験分布とすると、 $$ \mathbb{E}_{x\sim \hat{p}}KL(p_{w'} (y|x) || p_w (y|x)) = \delta w \cdot F\delta w + \mathcal{o}(\delta w^2) $$ ここで出てきた右辺のFが、フィッシャー情報行列(FIM)と呼ばれるもので、FIMは以下の式で定義されます。 $$ F = \mathbb{E}_{x,y \sim \hat{p}(x)p_w (y|x)} [\nabla _w \log p_w (y|x)\nabla _w \log p_w (y|x)^T] $$ 数式がややこしくなってきましたが、FIMは確率分布の各パラメータ毎の勾配を計算し、その転置行列との積をとっています。また、FIMは確率分布空間上のリーマン距離(計量)であり、 結合分布\(\hat{p}(x)p_w (y|x)\)についてのある特定のパラメータ(重み、特徴量)を含んでいます。 確率分布はベクトルで、それをパラメータベクトルで(偏)微分すると行列となります。この時、行列のi行目は確率分布の全ての値をi番目のパラメータで微分したものとなります。 つまり、FIMの対角成分のみが、同じパラメータで微分したものの二乗が並びます。
これより、FIMにおける対応するエントリ(成分)が小さい値なら、そのタスクはパラメータに強く依拠していないことが分かります。また、FIMはタスクの(コルモゴロフ)複雑性にも関係していると言われています。
以上のことよりFIMをタスクを表す指標としているわけです。
しかし、異なるネットワークでFIMを計算すると比較ができないため、本論文では前述した「probe network」を用います。 また上の数式からも分かるように、全てのパラメータに対する勾配を計算しなくてはならないため、計算量が多すぎるという問題点があります。 これに対応するために、本論文では2つの仮定を置いています。

1.「probe network」内の異なるフィルター間には相関がないと(暗黙的に)仮定→FIMの対角成分についてのみ考える
2.それぞれのフィルターの重みパラメータは基本独立していない→同じフィルターの全ての重みに対し平均化を行う

これによって結果的に得られたものは、「probe network」内のフィルター数と一致した固定長ベクトルであり、 このベクトルを使ってタスク間の距離を計算していくのです。 本論文11ページ目の「Analytic FIM for two-layer model」に簡単な二層モデルでのFIM導出を紹介しているので、 興味のある方は是非参照してみて下さい。

3.TASK2VEC 手順

さてやっと本題に入れるわけですが、まずTASK2VECは大きく次のステップに分けられます

1.事前学習済みモデルによって得られるFIMを計算【2.事前知識参照】
2.FIMの対角成分のみを取り出し、固定長のベクトルを出力

行なっている作業は基本これだけで他のモデルと比較する際に、この出力されたベクトル間の距離を計算します。

ベクトル間の距離計算

このベクトル間距離をユークリッド距離で計量しようとすると、1.ネットワークのパラメータは異なるスケールを持つ、 2.埋め込まれたベクトルのノルムは、タスクの複雑性や計算に使われたサンプル数の影響を受けるといった問題が発生するため、 本論文では距離計算の手法として次の場合分けを行なっています。

◎Symmetric TASK2VEC distance【対称性あり】:
$$ d_{sym}(F_a, F_b) = d_{cos}\left(\frac{F_a}{F_a +F_b}, \frac{F_b}{F_a +F_b}\right). $$ ここで対称性ありの場合について、距離計算の際の頑健性を保つためコサイン距離を導入します。
\(d_{cos}\)はコサイン距離(類似度)、\(F_a\), \(F_b\)は２つのタスク\(a, b\)をベクトル化したもの(計算によって得られたFIMの対角成分)を表しています。 それぞれ\(F_a +F_b\)で割って標準化していることに注意してください。 例えば、iNaturalistにおける種間の分類学上距離(Tax. distance)とコサイン距離について、 以下の図右より、完璧にはマッチしてないですがタスクサイズ\(k\)が大きいほど良い相関(関係)があることが分かります。

◎Asymmetric TASK2VEC distance【対称性なし】:
$$ d_{asym}(t_a \rightarrow t_b) = d_{sym}(t_a, t_b) - \alpha d_{sym}(t_a, t_0) $$ 次に非対称の場合についてですが、モデル選択の際は上記の転送距離(Transfer distance)が有効です。
一般的にImageNetのように複雑なタスク(データセット)から得られた学習済みモデルは良い性能を持っています。 本論文では、「タスクの複雑性は、"簡単なタスク\(t_0\)"の埋め込み表現によって得られるベクトルの大きさによって計算できる」 という考えをもとに、上記の計算式を導入しています。
この式が言わんとすることは、タスク\(a\)を用いてタスク\(b\)に転移学習させる際に、タスク\(a\)が複雑であればあるほど 良い結果がでるということです。つまり、タスク\(a\)とタスク\(b\)の類似性が高く、かつタスク\(a\)とタスク\(t_0\)の類似性が低いほど この距離は大きくなります。
ここで、\(t_a, t_b\)は2つのタスク、先ほど述べた\(t_0\)は簡単なタスク、\(\alpha\)はハイパーパラメータを表しています。 この\(\alpha\)はメタタスクをもとに選定されます。本論文の実験では、最適な\(\alpha\)がメタタスクの選定に関して 頑健性を持っていることが分かっています。(実験によるとprobe networkとして、ImageNetで事前学習させたResNet-34を使った時の\(\alpha\)は0.15)
【詳しくは本論文"3.1. Symmetric and asymmetric TASK2VEC metrics"参照】

MODEL2VEC【参考】

さて、上記のTASK2VECではタスク間の距離を算出することに成功しています。 しかしここまで読んでくださった読者様の中には、既にお気付きの方もいるでしょうがこのTASK2VEC、完全にモデルの詳細を無視してしまっています。
そこで、モデルが訓練されたタスクの埋め込みができるなら、そのモデルもベクトル化できるのではないか？と考えるわけです。
しかし、一般にそういったモデルの情報はブラックボックス化されてたりして分かりません。 そこで、同じタスクで異なる精度のモデルがあったら、タスクとモデル(アーキテクチャとトレーニングアルゴリズム)間の相互作用をモデル化するために、 2つの相互埋め込みを学習することを目標とすれば良いわけです。
具体的に本論文では、タスク空間に(似たタスク上でも良い精度を出すような)モデルを埋め込むために、メタ学習問題に関する次の公式を提唱しています。
\(k\)個のモデルが与えられた時、MODEL2VECによる埋め込み表現は、
$$ m_i = F_i + b_i $$ で与えられ、ここで\(F_i\)はモデル\(m_i\)をトレーニングするために使ったタスクをベクトル化したもので、\(b_i\)は学習済みの「モデルのバイアス」を表しています。
\(b_i\)は、タスク間距離によって与えられる最適なモデルを予測するための、k交差エントロピー誤差を最適化することによって得られます。 ここでタスク間距離は以下で定義されます。
$$ \mathcal{L} = \mathbb{E}[-\log p(m | d_{asym}(t, m_0), \cdots , d_{asym}(t, m_k))]. $$ トレーニング後、新しいタスクtが与えられた時、\(d_{asym}(t, m_i)\)を最大にするような\(m_i\)が最適なモデルというわけですが。。
あくまで参考程度に考えていただければ結構です。

4.論文の実験結果

使用データセット

まず本論文で使用するデータセットについて、簡単にまとめておきます。【右の数字はタスク数】

iNaturalist:生物を撮影した画像からなるデータセット。それぞれのタスクは種の分類タスクとなっている。【207】
CUB-200:鳥を撮影した画像からなるデータセット。それぞれのタスクは鳥類の分類タスクとなっている。【25】
iMaterialist:ファッション(服飾)画像のデータセット。服の分類に関するタスク(色、素材など)。【228】
DeepFashion:ファッション(服飾)画像のデータセット。iMaterialistと同じ、服の分類に関するタスク。【1000】

4つのデータ合わせて全1460のタスクで実験を行なっています。 これらのタスクで良い学習済みモデルを選択することに成功したTASK2VECですが、早速その実験結果を見ていきましょう。

学習済みモデル

先ほども述べましたが、本論文ではprobe networkとして、ImageNetで事前学習させたResNet-34を、 その後ファインチューニングしたものと、しないものとの2つで実験しています。

実験結果

本論文では4,100の分類器、156の特徴抽出機を使い、そして1,460の埋め込みを実験で行ったそうです(かかった時間は1,300GPU時間)。
再褐しますが、下図がiNaturalist, CUB-200, iMaterialistの3つのデータセットにおける各タスクを、t-SNEによって二次元のベクトルに落とし込み可視化したものです。(左図)
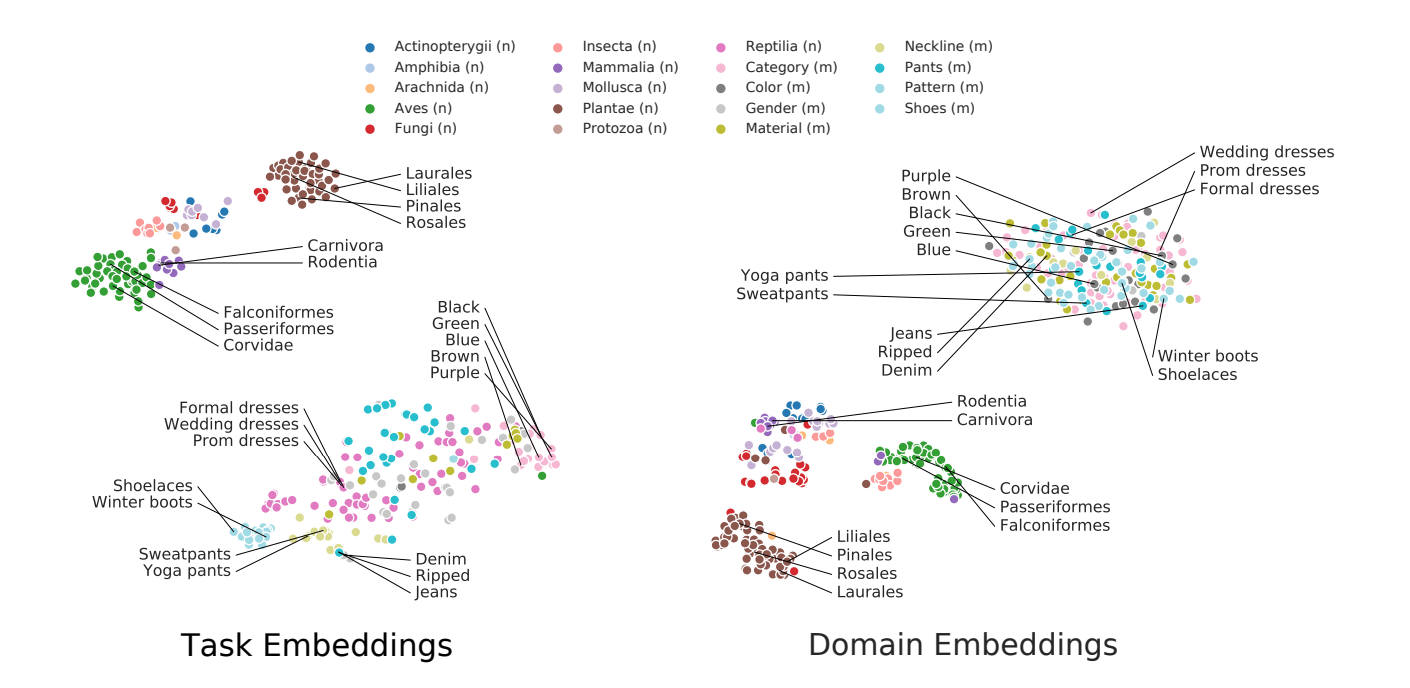
データセットと相関のあるタスク(例えばiMaterialistだったらパンツの分類タスクなど)は、そのタスク間がうまく分離できており、きちんとグルーピングできています。 しかし右図のように入力ベクトルのみによって埋め込まれたものは、iMaterialistのタスクは1つのクラスタとしてまとまっています。 つまり、データセット内のタスク間を分離できていないということです。 やはりTASK2VECの方がよくタスク間の分離ができていますね。

誤差分布

次にiNaturalistとCUB-200の156の学習済みモデルから特徴量を抽出し、そのタスクの分類誤差を示したものを見ていきましょう。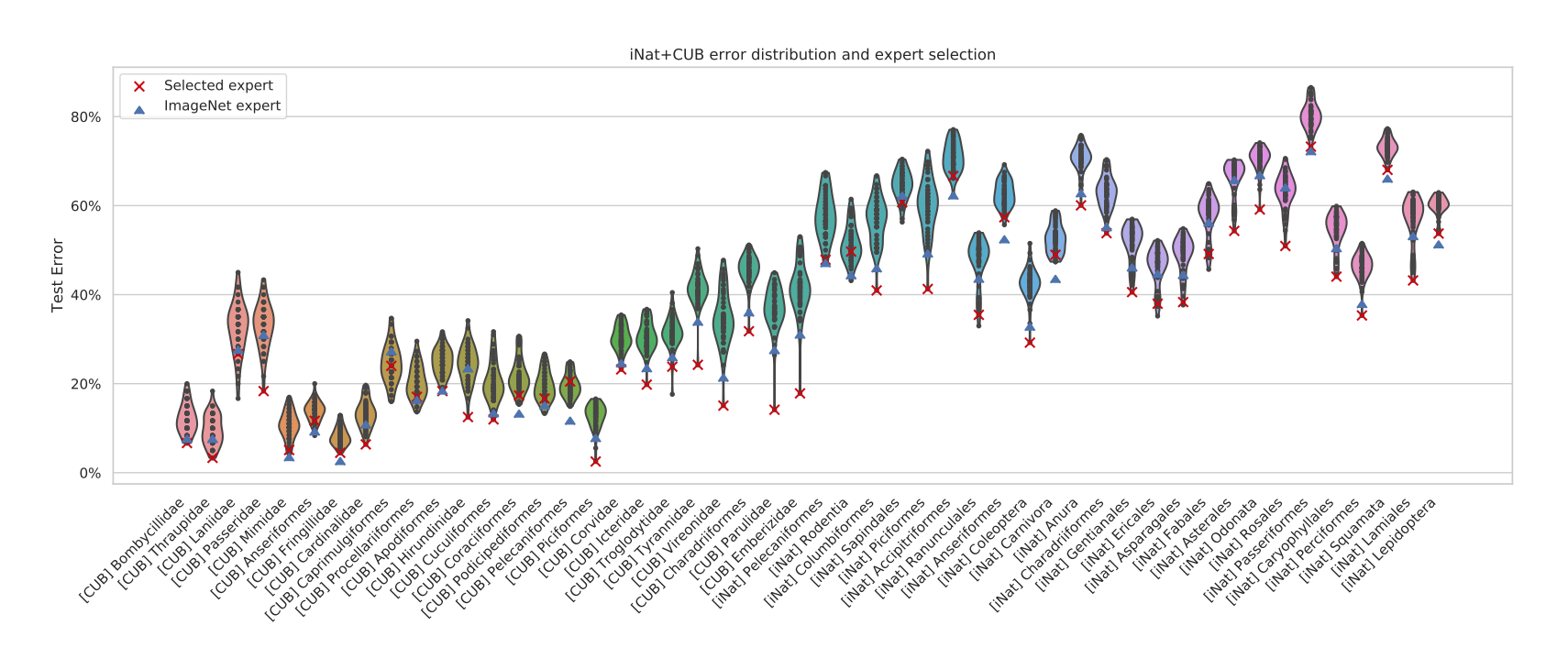
このヴァイオリン図において、縦軸はTest Error(テスト誤差)、横軸はそれぞれタスクを示しています。 赤の×がTASK2VECによってモデル選択を行なった場合の分類誤差、 青の△がファインチューニングしてないImageNetで事前学習させたものから抽出した分類誤差を表します。(赤×が低い値の方がいい)
まずこれらのタスクは、左から右へとベクトルのノルム(大きさ)が小さいものから順に並んでいます。 また右に行くに従って分類誤差が大きくなっていることから、TASK2VECによって得られるベクトルの大きさは、タスクの複雑性と正の相関があることが分かります。

サンプルサイズに対する依存性

私たちの興味のあるタスクが比較的少ないサンプル数しかない時、最適な特徴抽出器を見つけ出すことは特に重要になってきます。 次のグラフは、モデル選択においてサンプル数が変化した時、TASK2VECのパフォーマンスがどのように変わっていくかを表したものです。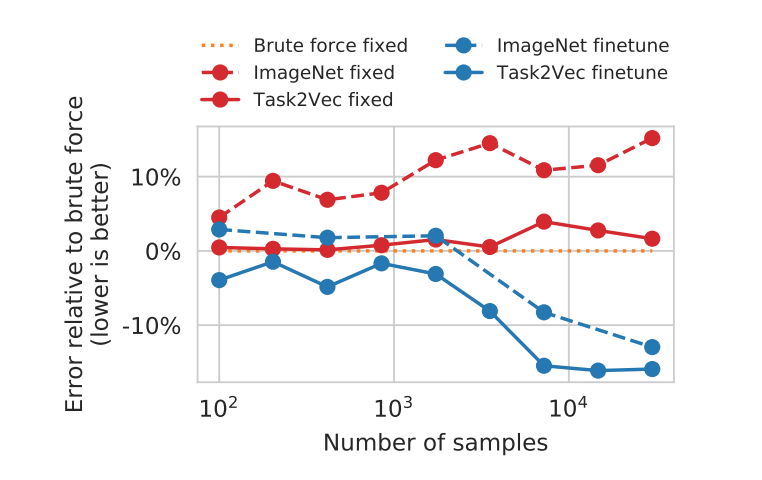 グラフはそれぞれ、
オレンジの点線:最も最適なモデルを選択した時
赤の実線:TASK2VECによって選択した特徴抽出器
赤の点線:ImageNetのみで事前学習させた特徴抽出器
青の実線:TASK2VECによって選択した特徴抽出器をファインチューニングしたもの
青の点線:ImageNetのみで事前学習させた特徴抽出器をファインチューニングしたもの
です。これより全てのサンプルサイズに対して、TASK2VECはImageNetのみで事前学習させたものより良い精度を出していることが分かります。
最後に、以下の最適誤差に関する表を見て下さい。 まずMeta-taskとして、iNaturalistとCUB-200の二つのタスクを合わせた「iNat + CUB」、全てのタスクを混合させた「Mixed」について考えています。 ここで「Chance」は適当なモデルを選択した場合に得られた特徴抽出器で、この表よりChanceのように安価な(何も工夫してない)特徴抽出器よりも、 ImageNetのみで事前学習させた特徴抽出器の方が良い精度であることが分かります。 しかし、そのImageNetのみで事前学習させた特徴抽出器よりも、TASK2VECを用いてタスク間距離を測定し、 モデル選択を行なった方が更に良い最適なモデルが得られることが分かります。

5.まとめ

TASK2VECはタスク、もしくは対応するデータセットを固定長のベクトルとして表現する有用な方法です。
性質として、
1.そのベクトルのノルムは、タスクのテスト誤差やタスクの複雑性と相関がある。
2.埋め込みによるベクトル間のコサイン距離は、タスクの自然距離(例えば種間の分類学上距離、転移学習におけるファインチューニング距離)と相関がある。
などが挙げられます。
総括すると、TASK２VECに基づくモデル選択のアルゴリズムは、学習なしに最適な(もしくは最適に近い)モデルを提唱するため、 自分で一から力尽くで(brute force)最適な学習済みモデルを探す必要がない！ということです。とても画期的な考えですね。 さて本論文にもありましたが、タスク空間上のメタ学習はこれからの人工知能に向けての重要なステップとなるでしょう。
実際、このTASK2VECは完璧にタスクの複雑性や多様性を捉えているわけではないので、実社会で見ることは少ないかと思います。 しかし、このTASK2VECの考え方を基に更なる発展のため、私も勉強していきます。

6.参考文献

TASK2VEC: Task Embedding for Meta-Learning
転移学習とは？ディープラーニングで期待の「転移学習」はどうやる？
データがないのに学習可能？　最先端AI「メタ学習」がスゴい