はじめに

ニューラルネットワークの学習の目的は、損失関数( loss function )の値をできるだけ小さくするようなパラメータを見つけることに他ならない。これは言い換えれば最適なパラメータを決定するという点で最適化問題に帰着されるが、ニューラルネットワークの最適化はそのパラメータの数の多さから大変複雑な問題として扱われる。

今回はSGD, Momentum, AdaGrad, Adamと呼ばれる4つのパラメータ更新手法を紹介し、最後にMNISTデータセットを用いてこれらの更新手法を比較していく。

※Pythonで用いているコードは『ゼロから作るディープラーニング(オーム社)』を参考にしている。

SGD(Stochastic Gradient Descent)

SGD(確率的勾配降下法)は、勾配方向へある一定距離だけ進むことを繰り返すという単純な方法である。以下はSGDのparameter更新式である。(以下、Lは損失関数)

但し偏微分は損失関数の勾配を表している。これをPythonのクラスとして実装すると以下のようになる。

確かに実装は簡単であるが、関数の形状が等方向でないと非効率な経路で探索してしまうという欠点がある。例えば、

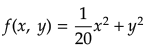
という関数についてこのSGDを適用してみよう(以下この関数を用いて各手法における最適化問題を解く)。その前にこの関数の形状及び勾配を下記に示す。

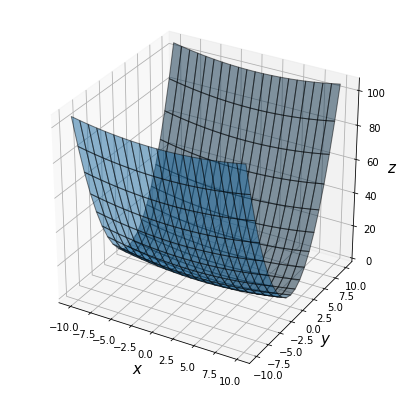
この勾配はy軸方向に大きく、x軸方向には小さいことが分かるだろう。しかし、今この関数の最小値は明らかに(x, y)=(0, 0)であるのに、上で示した勾配は多くの場所で(0, 0)方向を指していない。

実際、この関数にSGDを適用した結果(初期値(x, y)=(-7.0, 2.0))は以下のようなジグザグした動きをし、これはかなり非効率な経路である。

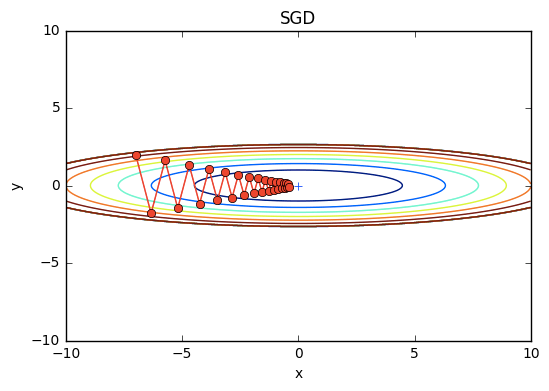
このSGDの非効率な探索経路の根本的な原因は、勾配の方向が本来の最小値ではない方向を指していることに起因している。 この欠点を改善するために、続いてMomentum, AdaGrad, Adamの3つの手法を紹介する。

Momentum

Momentumとは「運動量」という意味で物理を知っている人なら馴染みの深い言葉だろう。Momentumのparameter更新式は次のよう。

Momentumは簡単に言う\とSGDに慣性項αvを付与したものである。αはハイパーパラメータであり、前回の更新量にα倍して加算することでparameterの更新をより慣性的なものにする狙いがある。

今回もPythonのクラスとしてMomentumを実装してみる。

vは初期化時には何も保持しないが、update()が初めに呼ばれるときに、parameterと同じ構造のデータをディクショナリ変数として保持する。

ではこのMomentumを用いてさっきの関数の最適化問題を解いてみよう。結果は下図。

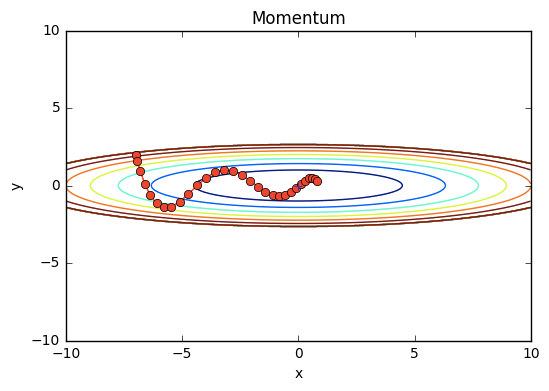
SGDよりもジグザグ度合いが軽減されているのは一目瞭然であるが、一体何故だろうか。x軸、y軸についてそれぞれ考えてみよう。

x軸方向: 受ける力は小さいが、常に同じ方向に力を受けるため、同じ方向へ一定して加速する

y軸方向: 受ける力は大きいが、正と負の方向の力を交互に受け止めるため、それらが互いに打ち消し合い、y軸方向の速度は安定しない。

これよりSGDのときと比べてx軸方向により早く近づくことができジグザグの動きを軽減できる。

AdaGrad

ニューラルネットの学習においてはラーニングレートηの値が重要になってくる。この値が小さすぎると学習に時間がかかりすぎてしまうし、逆に大きすぎても最適解にたどり着かずに発散してしまう。

このラーニングレートに関する有効なテクニックとして、学習係数の減衰( learning rate decay )という手法がある。これは簡潔に言うと、学習が進むにつれてラーニングレートを小さくするというものである。

最初は"大きく"学習し、次第に"小さく"学習する手法で、ニューラルネットの学習ではよく使われる。parameter更新式は以下のよう。

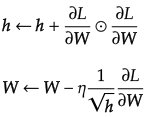
ここで、変数hにおいて⦿は行列の要素ごとの積を意味し、上式のように経験した勾配の値を2乗和として保持する。そして、更新の際に、hの二乗根で除算することにより学習のスケールを調整する。

これは、パラメータの要素の中でよく動いた(大きく更新された)要素は、ラーニングレートが小さくなることを表している。 実際にpythonのクラスとしてAdaGradを実装してみる。

最後の行で1e-7を加算しているのは、self.h[key]の中に0があったときに0で除算してしまうことを防ぐためのものである。 では実際にさっきの関数にAdaGradを適用してみよう。

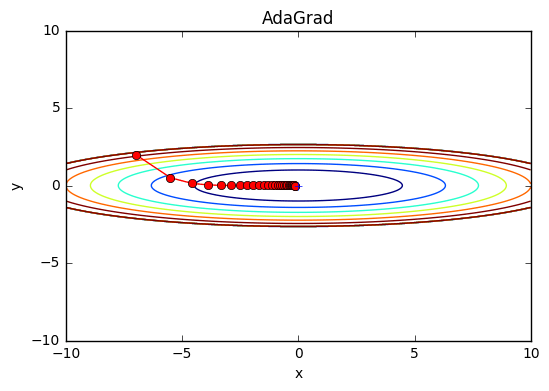
これより、さっきのSGD, Momentumよりも効率的に最小値に向かっているのが分かる。y軸方向には勾配が大きいため最初は大きな更新ステップとなっているが、その大きな動きに比例して更新のステップが次第に小さくなるように調整される。

Adam

Adamは2015年に提案された新しい手法であり、直感的にはMomentumとAdaGradを融合したような手法である。この2つの手法のメリットを組み合わせることで、効率的にparameter空間を探索することが期待できる。

また、ハイパーパラメータの「バイアス補正」が行われているのもAdamの特徴である。(詳細はこちらADAM: A METHOD FOR STOCHASTIC OPTIMIZATION)

更新式はやや複雑であるので、今回は割愛するが勾配降下法の最適化アルゴリズムを概観するに掲載してあるので、興味のある方はぜひ見てほしい。

実際にpythonのクラスとしてAdamを実装してみる。

Adamを用いて先の関数の最適化問題を解いてみよう。結果は以下のよう。

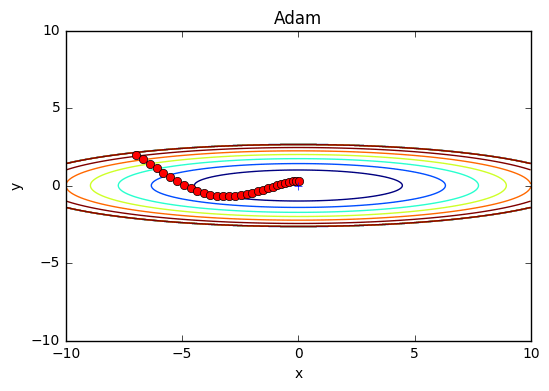
ソースコードは以下。

この比較実験では、5層のニューラルネット、各隠れ層100個のノードを持つネットワークを対象にした。また活性化関数としてReLUを使用した。

上のグラフより、SGDよりも他の手法のほうが速く学習できていることは見て容易だろう。さらにAdaGradのほうが少しだけ速く学習が行われているようである。

しかし、この実験はハイパーパラメータ(ラーニングレートなど)の設定や、ニューラルネット自体の構造(何層にするか)によって結果は変わってくることに留意せよ。

しかし、一般的にはSGDよりも他の3つの手法の方が速い学習を行い、より高い認識性能を誇ることもある。

以上4つの手法を紹介したが結局どれを用いるのがベストなのか？残念ながら全ての問題で優れた手法は今のところなく、それぞれに特徴があり、得意不得意な問題があるのが現状である。

実際、多くの研究において今でもSGDは用いられているし、他3つの手法も十分に試す価値がある。結局、自分の好きなように色々試して、最良の手法を見つけていく他ないであろう。

定期的にメルマガでも情報配信をしています。
ご希望の方は問い合わせページに「メルマガ登録希望」とご連絡ください。

参考文献

『ゼロから作るディープラーニング(オーム社)』

Optimizer:深層学習における勾配法について

各手法におけるパラメータ更新経路