新型コロナウイルス感染症とは？

2019年12月より中国で 新型コロナウイルス ( COVID-19 )による肺炎が発生し、2020年4月現在では日本国内でも急速に感染が拡大しています。

新型コロナウイルスは、感染症法における「 指定感染症 」、及び検疫法における「 検疫感染症 」に指定され、感染が確認された患者に対して入院措置などの法的処置を取ることが可能となりました。

今回は、まず感染の拡大等を予測できる感染症モデルについていくつか紹介していこうと思います。また、感染症拡大の指標である基本再生産数・実効再生産数についても、実際のコロナウイルスのデータを用いてみていきます。

感染症モデルと基本再生産数・実効再生産数

これまで私たちは、新型コロナウイルスをはじめとする様々な危機にさらされてきました。それを機に感染症の流行を抑えるべく、感染者の隔離による感染個体との接触回避や、ワクチン接種による免疫力の向上など様々な対策を講じてきました。一方、感染症の流行のメカニズムを定式化することにより得られる、感染症の数理モデルによる感染症の流行規模の予測も注目されています。

感染症の数理モデルとは、簡単に言うと「感染症がどのように伝播し、感染した人がどの程度の期間で発症し、どの程度の期間で回復するのか」といったプロセスを、数式によって記述したものです。

感染症モデルにも、そのプロセスをどのように仮定するかにより様々なものが存在します。今回はその中のいくつかを紹介していきます。

SIR model

SIRモデルは、感染症モデルの中で基本となるモデルで、原形はKermack-McKendrick(1927)によるモデルです。

　このモデルは、対象とする全人口を

• 感受性保持者（Susceptible）：感染症への免疫がなく、これから感染する可能性がある人
• 感染者（Infectios）：感染症に現在感染している人
• 免疫保持者（Recovered）：感染症から回復して免疫を持った人もしくは死亡した人
  

の３つの状態に分かれると仮定し、集団に感染症が広がる様子を表したモデルで、時間経過によるそれぞれの状態の個体数の増減を考えています。

ここでは感染症にかかった少数の人が、感染症にかかる可能性のある大きな集団と接触した場合を想定しています。

SIRモデルは以下の微分方程式により定式化されます。

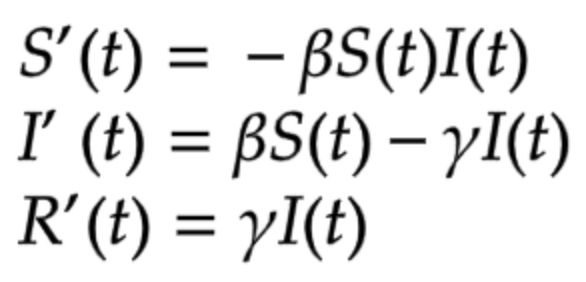
ここでS(t)、I(t)、R(t)はそれぞれ時刻tでの感受性保持者数、感染者数、免疫保持者数を表していて、微分方程式のそれぞれの式は微小時間での個体数の増減を数式化したものです。感受性保持者から感染者となる推移は両者が接触することを想定していることから、感受性保持者の減少及び感染者数の増加を表す式は、感受性保持者数と感染者数の積を用いて表現されています。

また、βは感染伝達係数、つまり感染率を意味するパラメータで、この値が大きいほど人から人へと感染しやすいこと表しています。

γは回復などで感染者でなくなる割合を表していて、感染症が治りやすければこの値も大きくなります。 ここで感染症が流行するというのは、モデル中のI(t)が増加することで、その条件は上のI'(t)の式から求めることができます。 初期値をI(0)、S(0)として、

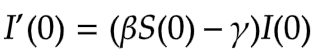
が正のとき、つまり

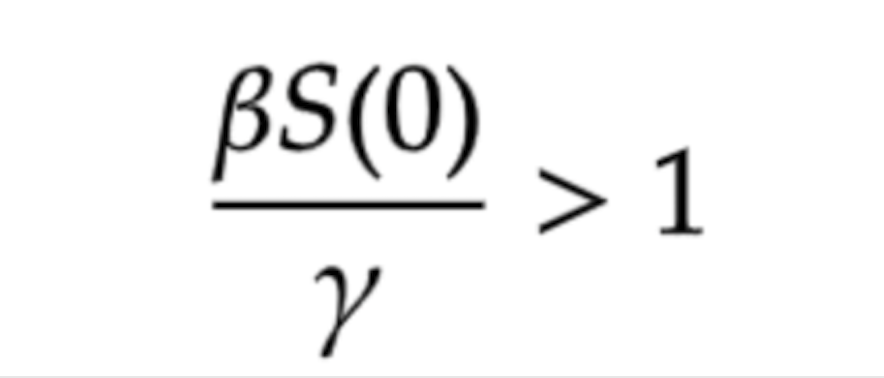
のとき、I(t)は初期時刻からの微小時間では単調増加で、ある時刻で最大値を取ります。最大値に到達した後は単調減少で0に収束していきます。 この値は基本再生産数と呼ばれます。ここで、基本再生産数について実効再生産数とともに簡単に説明したいと思います。

基本再生産数と実効再生産数

　基本再生産数とは、1人の感染者が感染力を失うまでに平均して何人の感受性保持者に直接感染させるのかという人数で、どの程度感染を広げる可能性があるかを示しています。 これは、

基本再生産数　=（単位時間あたりの2次感染者数)　×（平均感染期間）
　　　　　　　= 1次感染者が感染期間中に生み出す2次感染者数 と表すことができます。 またSIRモデルの式から、基本再生産数は

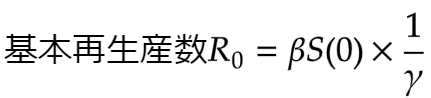
と表せます。

この値が

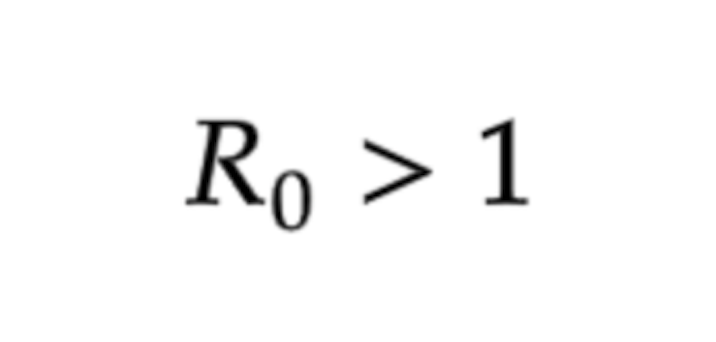
のとき感染症の流行が発生します。

基本再生産数を計算する一例を紹介します。

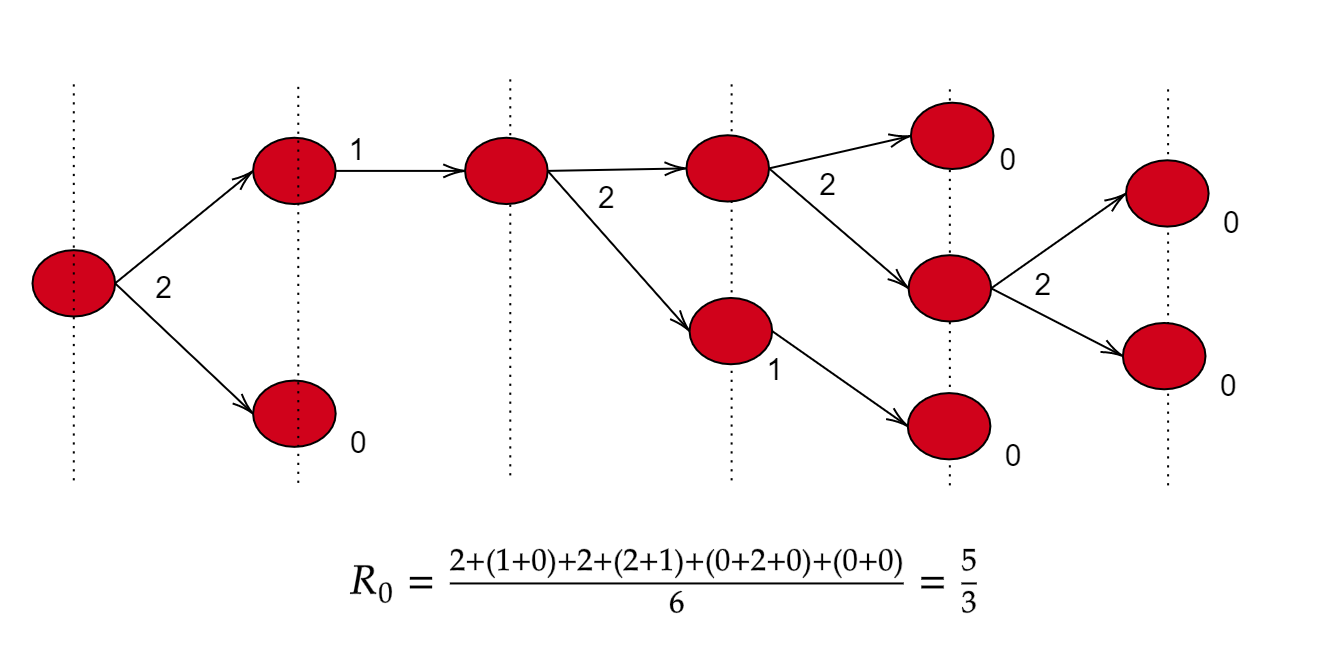
この図は、赤い丸が一人の感染者を表しています。一番左の時点を第１世代とし、その感染者が新たな感染者（第２世代）を生み出すとし、ここでは第６世代まで広がるとしています。一人の感染者が生み出す新たな感染者数は異なり、これが多いほど感染力の高い感染症であるとも考えられます。 ここで基本再生産数は

(全世代の新規感染者数)÷(世代数) で求めることができます。

ここで注意しなければならないのは、一般に基本再生産数の値は、一切対策を取らなかったときに感染症がどの程度感染を広げていく可能性があるのかを示すということです。

実効再生産数とは、感受性固体の一部が免疫化された集団の再生産数のことで、簡単に言うと、感染拡大しないように対策を取ったときの実際の再生産数のことです。感染症の流行を抑えるために、拡大防止対策を講じ、理論的には実効再生産数の値が1を下回れば感染の流行を収束に向かわせることができます。収束に向かわせるといっても、その期間の新たな感染者数が減少するということで、感染症が収まってなくなるというわけではありません。感染症の最終的な収束には、実効再生産数が大きくなりすぎないように対策を講じながら、集団免疫を獲得するかワクチン等の開発を待つ必要があるそうです。

基本再生産数の取る値により感染者数の増減はどのように異なるのでしょうか。

まず、基本的なSIRモデルの挙動は以下のようになります。

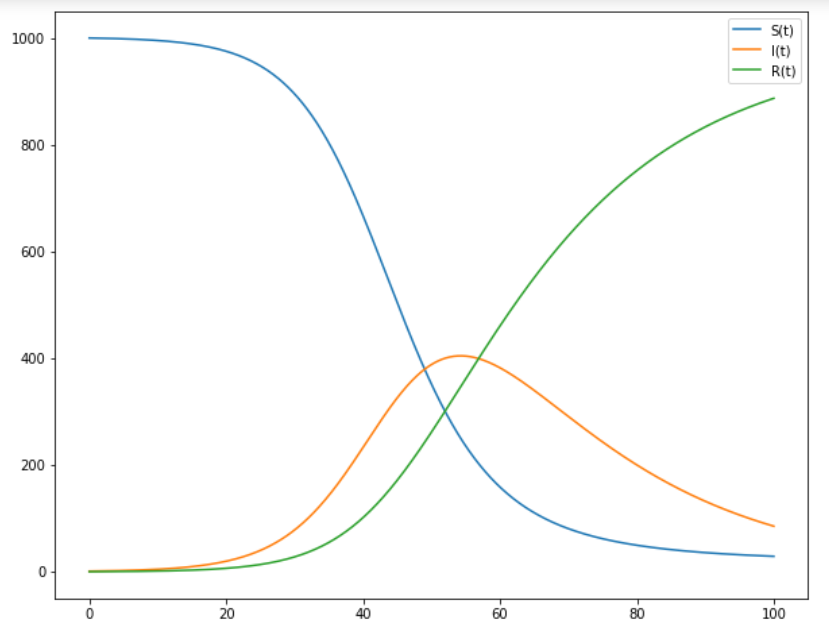
ここで注目するのは基本再生産数の値を40(β=0.2)のときと、4(β=0.02)のときの感染者数I(t)の推移を見てみます。

またγ=0.05、S(0)=10、I(0)=10とします。

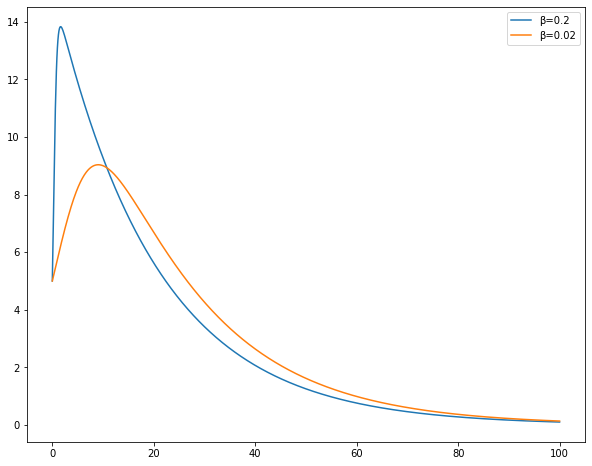
このグラフから、基本再生産数の値が大きくなると感染症の広がりが速くなり、そのピーク時の感染者数の最大値も大きくってしまうことが分かります。つまり、何も対策を取らなければ、感染症は急激に広がり、同時期に多くの感染者が発生してしまうのです。

次にSIRモデルから派生したSEIRモデルについて紹介します。

SEIRモデル

SEIRモデルとは、SIRモデルの3つの状態に加えて、潜伏期感染者(Exposed)を考えたモデルです。

つまり、対象とする全人口を

• 感受性保持者（Susceptible）：感染症への免疫がなく、これから感染する可能性がある人
• 潜伏期感染者（Exposed）：感染症に感染したが潜伏期間で、感染力がない人
• 感染者（Infectios）：感染症に現在感染している人で、感染力がある人
• 免疫保持者（Recovered）：感染症から回復して免疫を持った人もしくは死亡した人
  

の4つの状態に分かれると仮定し、集団に感染症が広がる様子を表したモデルで、時間経過によるそれぞれの状態の個体数の増減を考えています。 今回のコロナウイルスを簡単に見るときにはSEIRモデルがよく使われているような印象です。

SEIRモデルは以下の微分方程式により定式化されます。

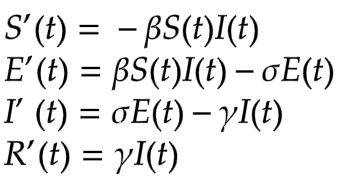
ここでS(t)、E(t)、I(t)、R(t)はそれぞれ時刻tでの感受性保持者数、潜伏期感染者数、感染者数、免疫保持者数を表していて、微分方程式のそれぞれの式は微小時間での個体数の増減を数式化したものです。ここでSIRモデルで無かったパラメータσは潜伏期間から感染状態へ移行することを表す係数で、単位時間あたりの発症率を表します。

SEIRモデルの挙動は以下のようになります。

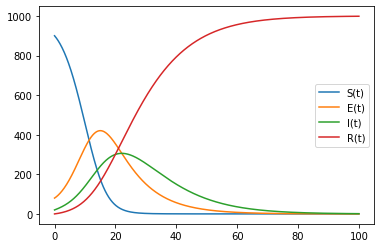
次にSISモデルについて説明します。

SISモデル

SISモデルは、感受性保持者（Susceptible）と感染者（Infected）の2つの状態のみを考えます。感受性保持者から感染者へ移行するのはSIRモデルと同じですが、SISモデルでは感染してから回復した後に免疫を獲得せずに、再び感受性保持者になり、感染の可能性がある状態へと移行すると考えています。

SISモデルは以下の微分方程式により定式化されます。

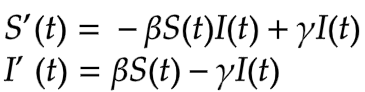
ここでS(t)、I(t)はそれぞれ時刻tでの感受性保持者数、感染者数を表していて、微分方程式のそれぞれの式は微小時間での個体数の増減を数式化したものです。また、ここで出てくる係数はSIRモデルと同じです。SIRモデルと比べると、感受性保持者から感染者へと移行する様子が良く分かると思います。

SISモデルの挙動は以下のようになります。

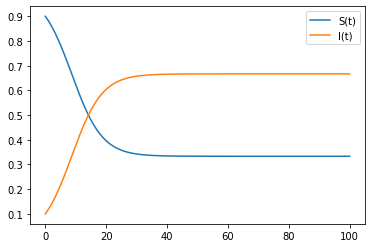
グラフを見て分かるように、ある程度まで感染者が増えると、感受性保持者と感染者の数が一定になります。つまり一定になってからは、感受性保持者と感染者の状態を一定数が行き来しているということになります。

これらの感染症モデルを見ていると、感染症による状態の遷移をどのように仮定するかでモデルが決まることが分かると思います。これら以外でも、違う仮定をすることで感染症モデルは提案がされていますし、感染症ごとにモデルを検討されることもあると思います。

感染症モデルを用いることで、感染症が出てきた段階では、どの程度広がっていくのかスピード等も考慮しながら予測することができ、対策を講じる際に利用することができます。また、対策を講じた後もどの程度効果があったかや、その先対策を講じながらの感染者の推移について予測する際にも用いることができます。

また実際に感染がどの程度抑えられているかは、実効再生産数を算出することで確認できます。

コロナウイルスデータの実効再生産数の推移

実際のコロナウイルスの感染者数データから、実効再生産数の推移を見ていこうと思います。実効再生産数については上で紹介しましたが、計算法についてはいくつかあるようで、今回はCoriらの論文にあるエクセルシートを使いました。データについてはsignateのCOVID-19 Challengeで与えられている都道府県ごとの感染者数データを使っています。本来、実効再生産数を計算する際には検査数等も考慮する必要があると思いますし、実際に専門の方が計算するのとは差があり、あまり正確な値ではないので、参考程度に考えてください。

ここで推移を見るのは、北海道・東京・大阪・愛知としました。愛知県のみ、５月１４日で緊急事態宣言が解除されています。（５月１９日時点）

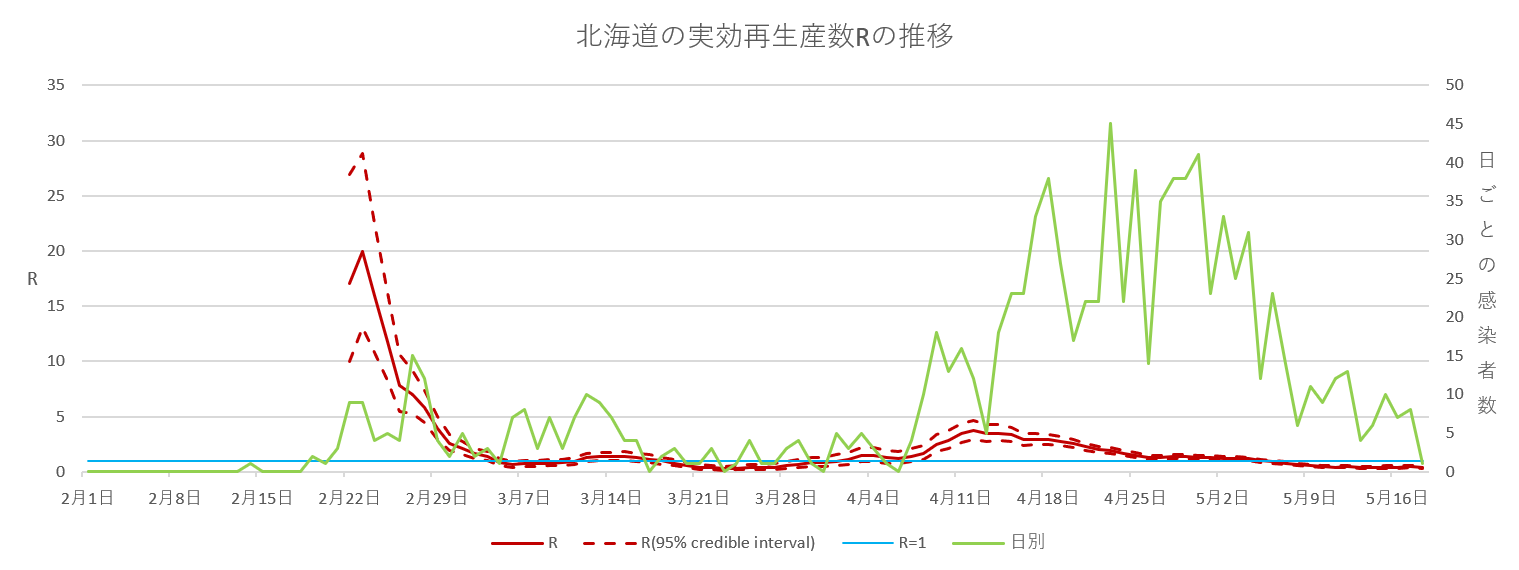
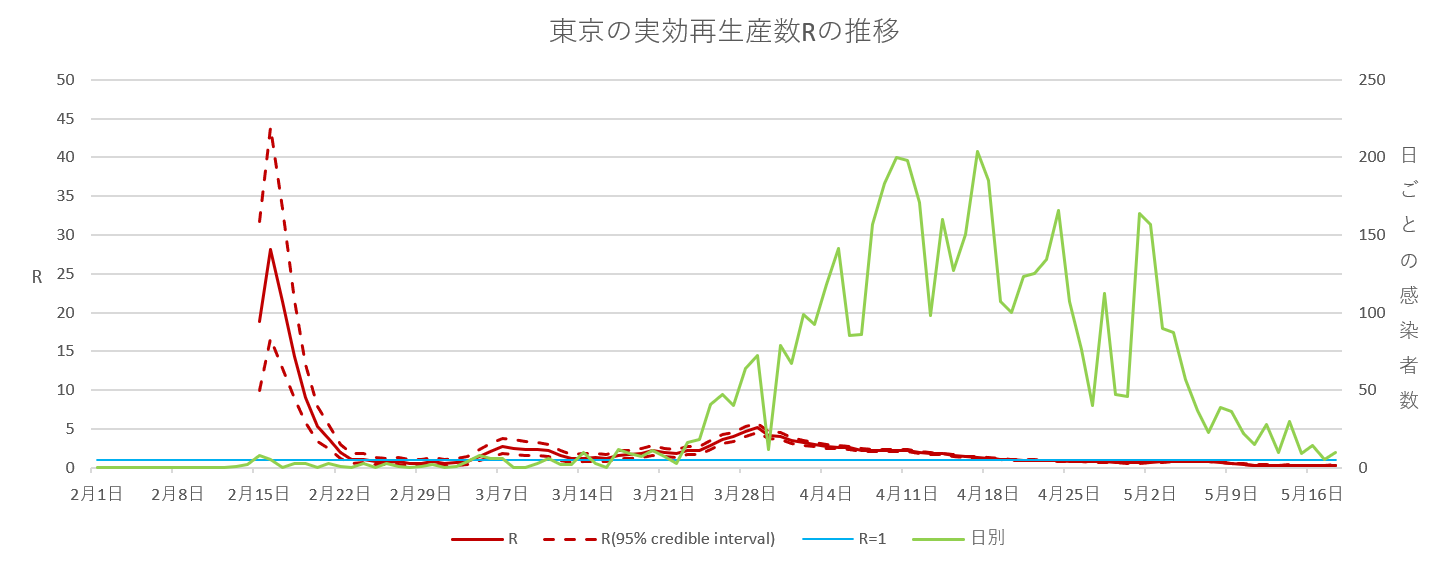
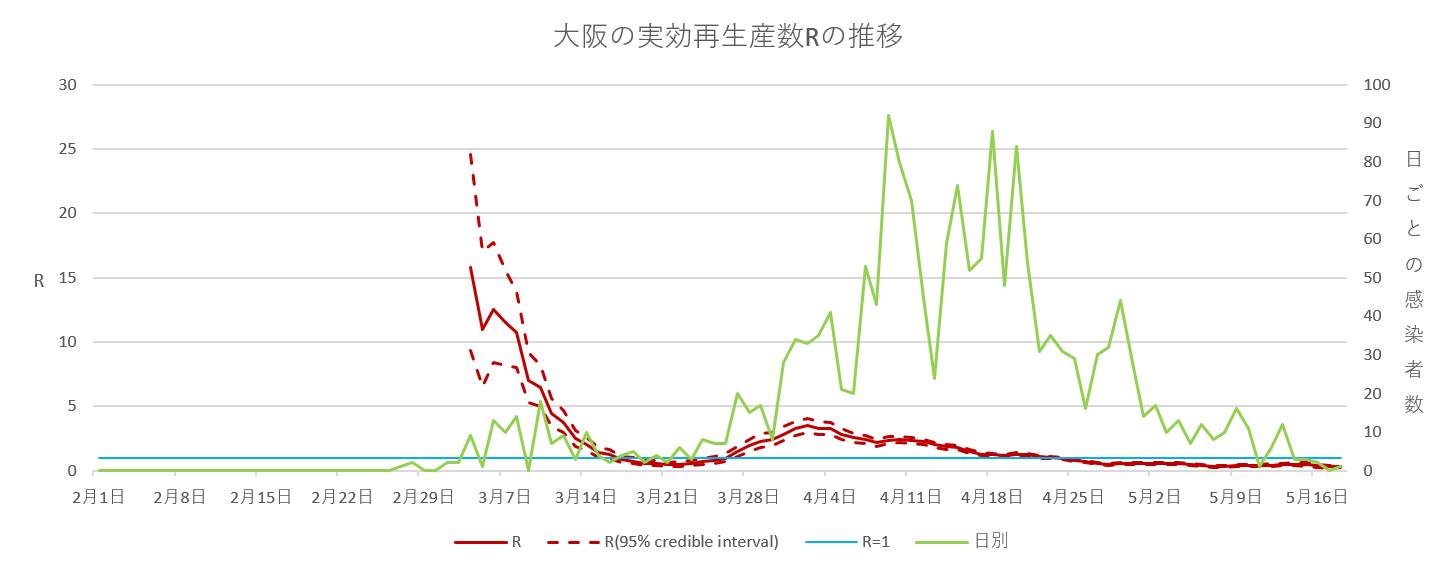
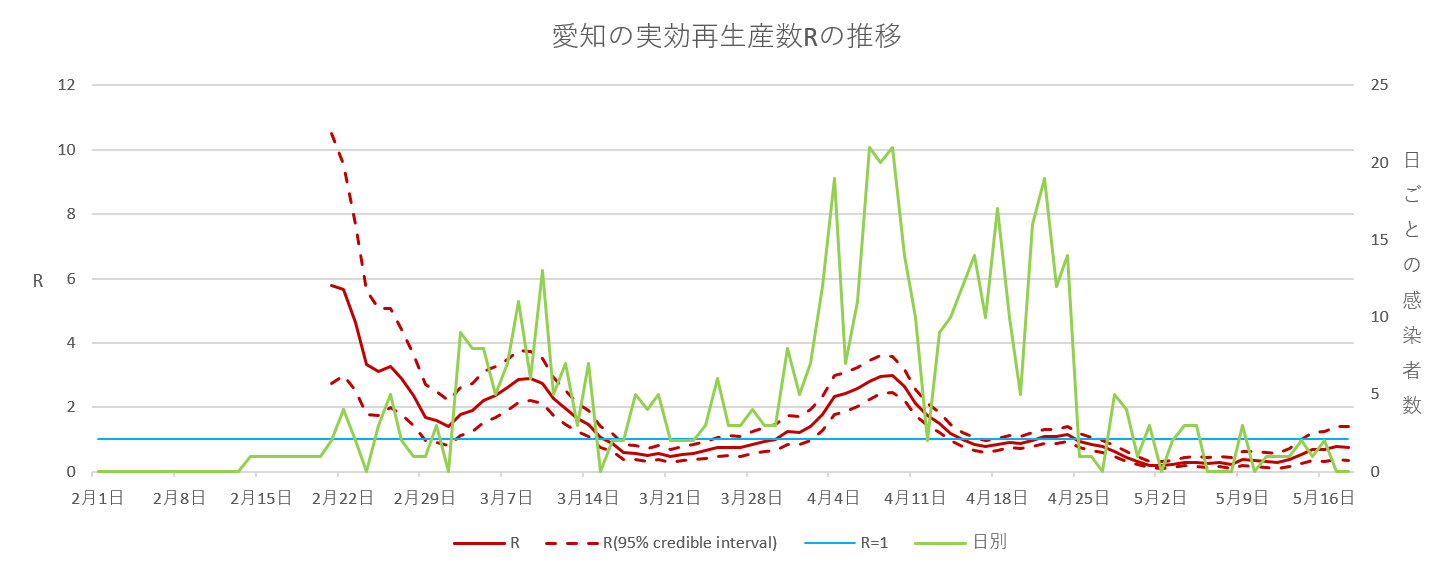
グラフを見るポイントは、実効再生産数が１未満に抑えることができているかということです。それぞれ見ると５月１９日時点で、すべて実効再生産数１を下回っているので、感染の広がりをうまく抑えられているように思います。

推移の中で、実効再生産数が１を下回り安定し始めたの日は、北海道が５月５日ごろ、東京・大阪が４月２１日ごろ、愛知が４月１５日ごろとなっています。一足先に緊急事態宣言が解除された愛知が、少しですが他よりも早く実効再生産数が下がった印象です。また東京・大阪にくらべて、北海道は実効再生産数が１未満に下がるのが遅い印象なので、緊急事態宣言の解除等に影響してくるかもしれません。

あくまでも参考値であるものの、今回見た地域では実効再生産数が５月１９日時点で１を下回って少し落ち着ているので、少しずつ自粛緩和 は進んでくるとは思います。ただしグラフを見て分かるように、少し前の時期には実効再生産数が１を大きく上回っています。また、今の状況というのは強めに自粛を呼び掛けての結果ですので、実際に少し前の時期には実効再生産数が１を上回っていた事実をデータから受け止め、簡単にその状態に戻ってしまうことを肝に銘じておく必要があると思います。

まとめ

今回はコロナウイルスの流行により注目されている感染症モデル等について紹介しました。日々状況が更新される中で、実効再生産数等はこれからも対策をとる一つの指標となるので、正しく理解することが大切です。

Twitter・Facebookで定期的に情報発信しています！
Follow @acceluniverse