DEVELOPER’s BLOG
技術ブログ
［機械学習 × 音楽］MIRとよく使われる特徴量
はじめに
現代社会には、音楽というものが氾濫しています。
そして多くの人は音楽を聞くというと、生演奏されているものを聞くことよりもCDやサブスク型サービスなど、一度デジタルなデータになったものをアナログデータへ変換して視聴することの方がよっぽど多いでしょう。
このデータ化によって普段聞いているだけでは気づかないような、特徴、性質に目を向け、そういった見えなかったデータを使い既存のものをもっと充実させる、新しいものを作り出すことはできないでしょうか。
この記事ではそういった取り組みや手法の一端を紹介できればと思います。
目次
MIRの現状
こういった音データ（特に音楽）から情報を抽出、分析する分野は、MIR(Music Information Retrieval)と呼ばれています。 ISMIRという世界規模のMIRに関する研究が発表される学会があり、2019年は20周年という大きな区切りの年でした。しかし、そこで発表された論文の一つの中で法的制限によって研究が進めづらく、また大企業とそれ以外とで資金面の違いから多様な研究が阻害されることによる再現性の危機等が指摘されています。 また、日本のGoogleで2019年11月現在MIRでと検索しても１ページ目に音楽分野のMIRの記事は出てこなく、あまり広く普及しているとはいえないのが現状でしょう。（MIRという略語が他にも多く当てられているということもありますが・・）
特徴量
このブログは技術ブログなので実際に使われている特徴量（データを扱う際にデータの特性を数値にしたもの）、またその抽出に関していくつか紹介していきます。
ここでは例としてヴィヴァルディの四季から春の第１楽章と冬の第２楽章のデータを扱っていきます。
Spring
Winter
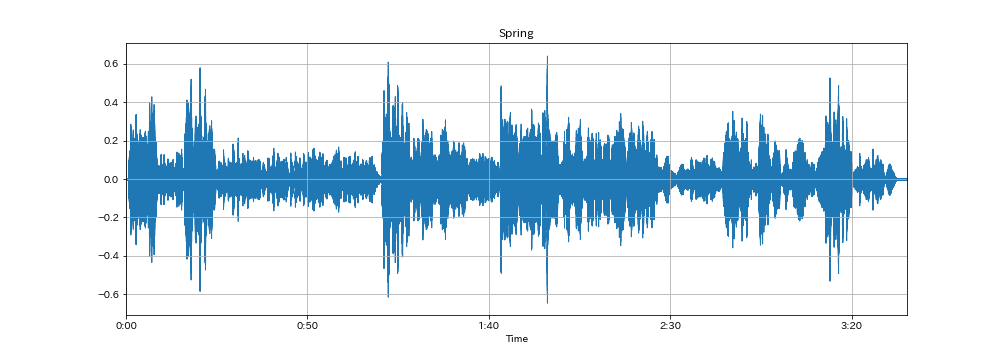
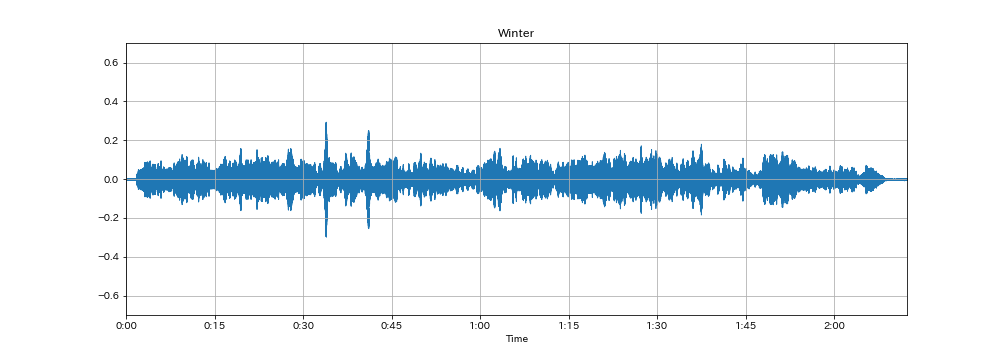
下グラフは、それぞれの信号をサンプリング間隔(sr=22050)でグラフ化したものです。 春は振れ幅が大きいところと小さいところがはっきりと分かれているのがわかります。 一方、冬は全体的に振れ幅が小さく、また曲自体も穏やかな印象を受けます。
1．平均平方２乗エネルギー(Root Means Square Energy)
EがErrorではなくEnergyなので読むときに注意が必要な値。単にRMSと書いている場合もあります。
表すものは単純にその音楽がどのくらいのエネルギー（音の大きさ）をもっているかをあらわし、下記スペクトル流動と相性が良いとされています。
オリジナルの波とそのまま比べると大きさだと見比べづらいので、0-6秒までをプロットします。
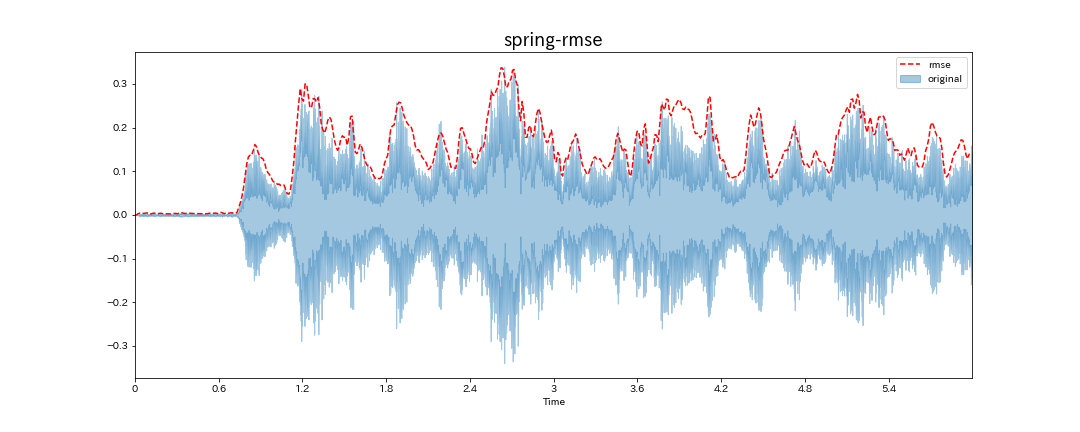おおよそオリジナルの波と同じ形を描いています。
エネルギーが大きいところは、激しいと読み替えることができるように思えます。しかし、その考え方でこの特徴量を利用すると大きな落とし穴があります。
春のヴァイオリンソロ部分（1:57〜）は、オリジナルの波を見てみると、振れ幅が小さくなっています。
しかし、だからといって穏やかなわけではありません。しかし、rmseを使うと、ソロパートなど、合奏に比べ音量が負けやすいところは数値が小さくでてしまいます。
結局、この特徴量はどれだけ音が大きいかということしかわかりません。
2．ゼロ交差率(Zero Crossing Rate)
音の波が正から負に変化する頻度を表した数値で、ノイズ量（不安定さ）を表す一つの手法とされています。
オリジナルのグラフは、波が潰れてしまっているので拡大して見てみます。
Springの１秒からsr=300まで（約0.01秒）ののグラフです。
波が単純でないので分かりづらいですが、この区間の場合だとZCR=8となります。
しかし、高音は元々波の間隔が狭いため、高音が多い曲では適切に動作しません。
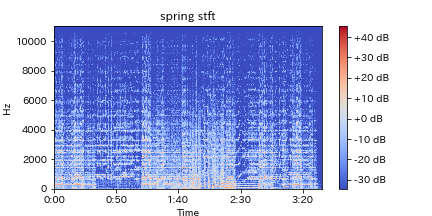
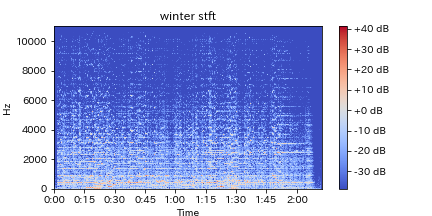
3．短時間フーリエ変換（Short Time Fourier Transform: STFT）
曲によって演奏時間は違い、それらの異なる長さのデータを扱うために、一定の時間（短時間）に対して離散フーリエ変換（一般的に高速フーリエ変換）を行い、それを繰り返すことによって、どのように曲が展開されているかを知る手法です。
フーリエ変換の概要については、省略しますが、簡単に言うと、オリジナルのグラフのように振れ幅（正確には無次元量）と時間軸で表されているものを、一定の時間内に、どのくらいの強さの振動がどのくらいあるかに変換する手法です。
STFTによって求められる周波数スペクトル（どの周波数の音がどれくらいあるか）を用いて下で紹介するようなMSCCなどへと発展できます。
4．定Ｑ変換（Constant-Q Transform）
STFTでは扱う時間を増やすと多くの周波数を含むことができる可能性があるため一般に周波数分解能は高くなりますが、時間間隔が長いためにその中で起こっている変化をとらえにくくなるというジレンマを抱えています。
定Ｑ変換では、この問題に対応するために分析する周波数間隔を人間の耳が感じているとされているように対数的に設定します。
つまり、人間の耳と同じように特定の周波数（低域）に対しては敏感に分析し、そうでないところ（高域）は荒く分析対応するのが、定Q変換の考え方です。
これによって効率よく必要なデータ分析が行なえます。
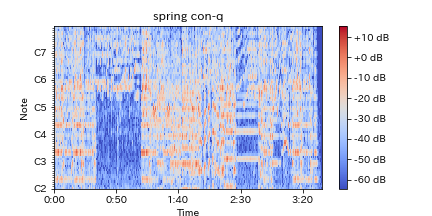
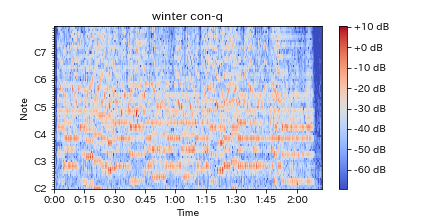
上記フーリエ変換後のスペクトログラムに比べ人間の耳に聞こえやすい音域が強調され広がっているのがわかります。
C4はト音記号の一番低いド（普通のド）で、 約261.626Hzとされていて、オクターブ上がるごとに約倍音（平均律のため誤差が生じる）になります。
5．ログメルスペクトログラム（Log-melspectrogram）
単にメルスペクトログラムと言われていることもあります。
上記1や2（１が主流）で得られた振幅スペクトルをメル尺度（実際の音と人間の音高知覚の差異を吸収したもの）で扱うためにメルフィルターバンクを適応たものです。
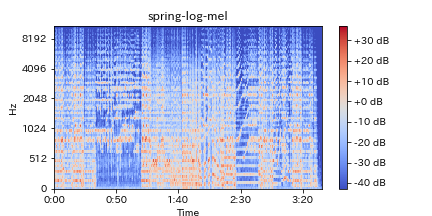
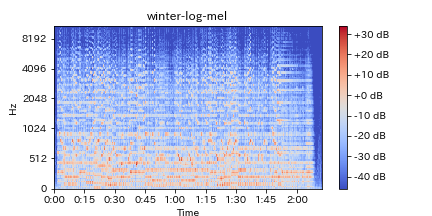
前提となる考え方が定Qと同じく人間の耳に適応させた特徴量を作り出すことを目的としているためスペクトログラムは似ていますが、低域に対してブーストされていないため、定Qを下にずらした形となっているのがわかります。
6．メル頻度ケプストラム係数（Mel Frequency Cepstrum Coefficients: MFCC）
ケプストラム(Cepstrum)はスペクトル(Spectrum)の最初の4文字をひっくり返した造語とのことで、スペクトル信号をフーリエ変換した結果であるそうです。
上記３の値を離散コサイン変換し、その値の低次元成分部分で構成されています。
また、この値はもともと喋り声などのデータに使われていた特徴量で、離散コサイン変換の段階で空間的特性を削除するため、ディープラーニングの際に適さないのではないかという主張もあります。
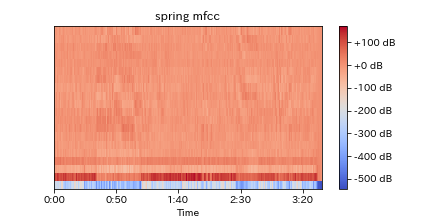
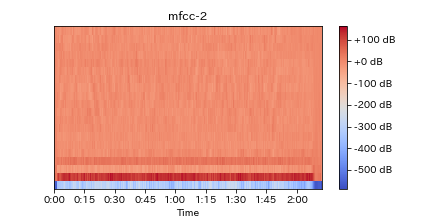
たしかに、定Qやログメルと比べると変化のある面積が少なくなっています。
機械学習×音楽の実用例
ずらずらといくつか紹介しましたが、一体これらの値を用いてどういったことができるのでしょうか。
例えば、今音楽を聞く手段として、ひとつの主流な形になっているものとしてサブスクライブ型サービスがあります。
定額で契約期間中数千万曲の中から好きなだけ好きなものを聞けるという画期的なサービスです。
しかし、やはりこれだけの曲数があると何を聞くか迷い結局同じ曲を聞くにとどまることが多いでしょう。
そこで各社は、様々な方法でレコメンド機能を実装しています。多くは、その曲を聞いた他の多くのユーザーがよく聞いている曲が選ばれています（協調フィルタリング）。しかし、これでは話題の曲など普段そういった曲を聞かないような人も聞いている曲では正しいおすすめはできないでしょう。
音楽サブスクライブ配信大手のSpotifyではこれに加え、音声データを用いた学習を活用しています。純粋にその曲に似ている、同じ雰囲気の曲を探しだし、Discover Weeklyで他社に先んじた高精度のレコメンド機能を提供しています。
また、今年の3月にgoogleが適当に音を数個与えるとそれに対して和音を足して"バッハっぽい音楽"を作り出すというシステムを発表しました。
このように機械学習は、既存のものを踏襲しつつ新たなものを発見したり生み出すことができ、今まで気が付かなかった可能性にも気づかせてくれるのです。
定期的にメルマガでも情報配信をしています。
ご希望の方は問い合わせページに「メルマガ登録希望」とご連絡ください。
参考文献、使用音源
The Four Seasons(Vivaldi) by John Harrison with the Wichita State University Chamber https://freemusicarchive.org/music/JohnHarrisonwiththeWichitaStateUniversityChamberPlayers/TheFourSeasons_Vivaldi 協奏曲第1番ホ長調 RV 269「春」（La Primavera）第1楽章 協奏曲第4番ヘ短調 RV 297「冬」（L'Inverno） 第2楽章
関連記事
目次 背景 原因究明 解決策 結果 背景 AUCでは、SRE活動の一環として、AWSコストの適正化を行っています。 （技術ブログ『SRE：コスト抑制のための異常値検知機構の実装』） コスト適正化における課題は、大きく分けて下記の4つです。 ①コストは月末にチェックしており、月中でコストが急激に上昇した場合発見が遅れてしまう。 ② 不要なリソースが放置されていたり、新たなリリースによって生じたコストを確認していない。 ③ AWSが提供するベスト
目次 実装前の課題 採用した技術と理由 実装した内容の紹介 改善したこと（抑制できたコスト） 実装前の課題 SRE（Site Reliability Engineering：サイト信頼性エンジニアリング）とは、Googleが提唱したシステム管理とサービス運用に対するアプローチです。システムの信頼性に焦点を置き、企業が保有する全てのシステムの管理、問題解決、運用タスクの自動化を行います。 弊社では2021年2月からSRE活動を行っており、セキュリ
目次 AUCの使用ツール GitHub、CircleCI使用までの流れ AWSの構成図 まとめ AUCの使用ツール 弊社ではGitHubとCircleCIの2つのツールを利用し、DevOpsの概念を実現しております。 DevOpsとは、開発者(Development)と運用者(Operations)が強調することで、ユーザーにとってより価値の高いシステムを提供する、という概念です。 開発者は、「システムへ新しい機能を追加したい」 運用者は、「システムを
2022年卒大学生の皆さん！ コロナウイルスが流行していることで就活にどういう影響があるのか、とても不安ですよね。 今回は業界ごとに採用人数を予測し、「どの業界が狙い目なのか」機械学習を使った分析手順を紹介します！ 目次 概要 手順 今後の課題 1.概要 データセットの内容 分析対象の7業界・各4企業 化粧品 電子機器 商社 不動産 金融 サービス IT・情報 説明変数と目的変数 特徴量 年初の株価、決算報告書提出翌日の株価、一株あたりの純資産額、従業員数