はじめに

クラスタリングはマーケティング手法としても使われている。
見込み顧客へ適切な施策を行うために、似た顧客同士をカテゴリ分けする必要があり、それをセグメンテーションという。
セグメンテーションのために機械学習の手法としてクラスタリングが使用されている。

k-meansクラスタリング（以下、k-means法）は複数個のデータをcentroids(重点)からの距離に応じて、あらかじめ決めたk個のクラスタに分ける非階層クラスタリング、及び、ハードクラスタリングの手法の１つである。

階層・非階層クラスタリングの詳細については以下のブログを参考にしてほしい。 （アクセルユニバース株式会社技術ブログ、富田、2019）

クラスタリングのため目的変数無し（ラベル無し）の場合のみこの手法は利用可能である。本記事は「k-means法とはどういったものか」に焦点を当て、方法やその過程について書いている。そのため数学的な要素は最小限に留めている（k-means++法やシルエット関数の計算方法等）。これらの数学的アプローチは今後の記事、もしくは、後述の参考文献をご覧いただきたい。

k-means法の実行方法

まず最初に各データからそれらが属するクラスタの重点までの距離を定義しなければならない。クラスタは全データの中で似たもの同士の集合体であり、その判断は各データから重点の距離を基に行われる。これにはsquared Euclidean distance (ユークリッド距離の２乗)がよく使われる。他にもユークリッド距離を用いたクラスタ内誤差平方和(SSE)を最小化する方法や、マンハッタン距離、マハラノビス距離等も使われており、データ分析の当事者が最適だと考えるものを選ぶ。

各データから重点のユークリッド距離の誤差を最小限にする方法の一例。引用元：　(https://data-flair.training/blogs/k-means-clustering-tutorial/)

次にクラスタの数を決める。K-means法を行う際にはあらかじめ全データを何個のクラスタに分けるか定める必要がある。この個数に関して最適解は無く、データ分析者自身が判断しなければならない。極端に言えば、データ分布を観た後に直感的に個数を決めてもそれが間違っているのかどうか分からない。しかしながら、もちろんそれでは説得力に著しくかける。求められているのはクラスタ内誤差平方和(SSE)を最小化するなどして、できるだけ類似度の高いデータを集めたクラスタ数を決める。以下のような方法がより良いクラスタ数を導き出すために使われている。

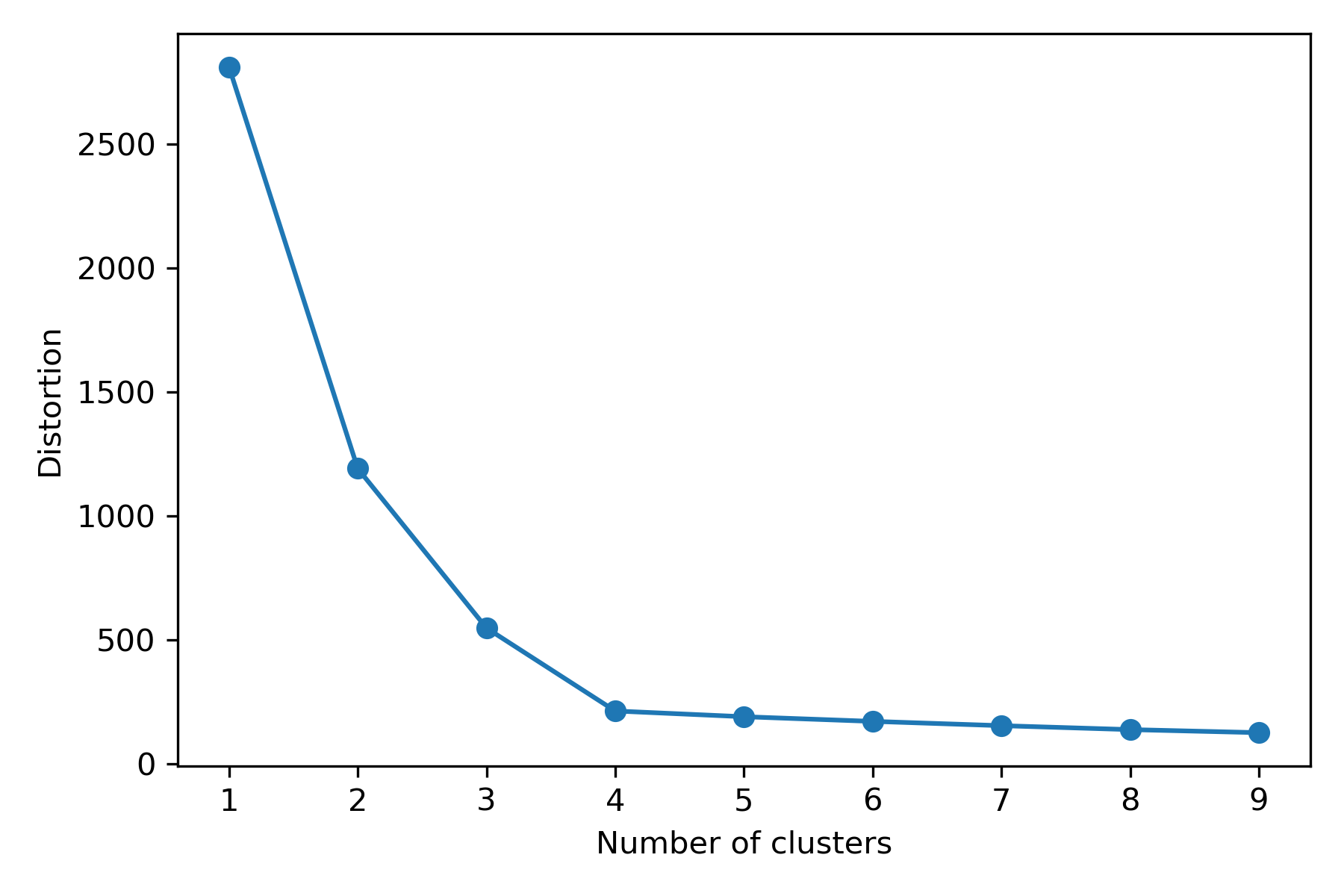
・エルボー法（elbow method） SSEから判明する歪みに基づき、最も適したｋの個数を導き出す方法である。歪みの最も大きくなった地点のｋを最適解と見なす。下記の場合はk＝4。

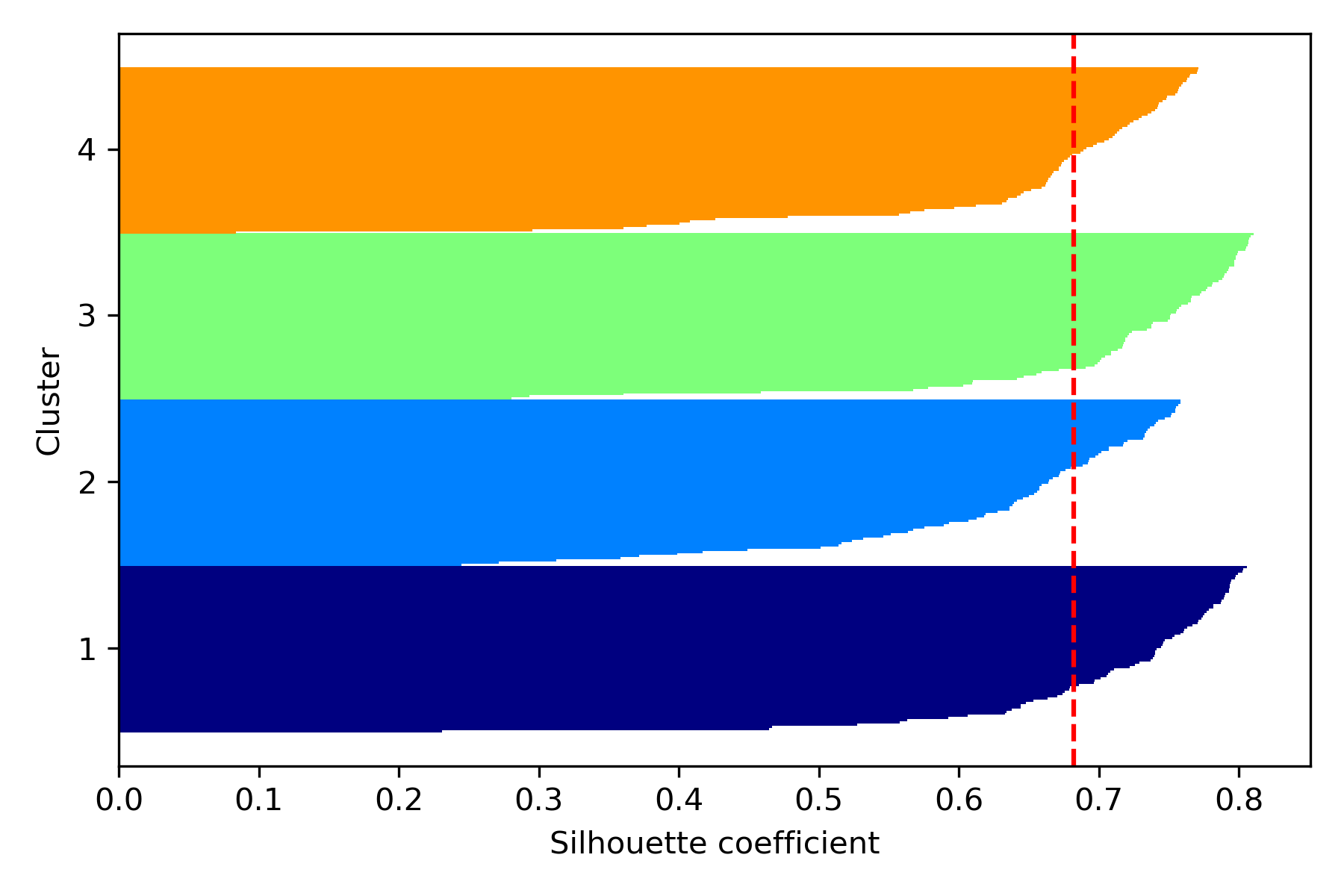
・シルエット法 (silhouette method) シルエット分析(silhouette analysis)とも呼ばれ、クラスタ内のデータの密度をプロット化し、最適なｋの数を判断する。シルエット係数(silhouette coefficient)は−１から１の範囲で表され、１に近いほどクラスター間の距離が遠く、しっかりとクラスターが分けられていることを表す。各バーがおよそ均等な幅になるようにクラスタ数を設定する。

以上のような方法でクラスタ数を決めたら、各クラスタの重点が動かなくなるまでになればk-means法は終了である。

k-means法のためのPythonコード(Hastie *et al*., 2017 参照)

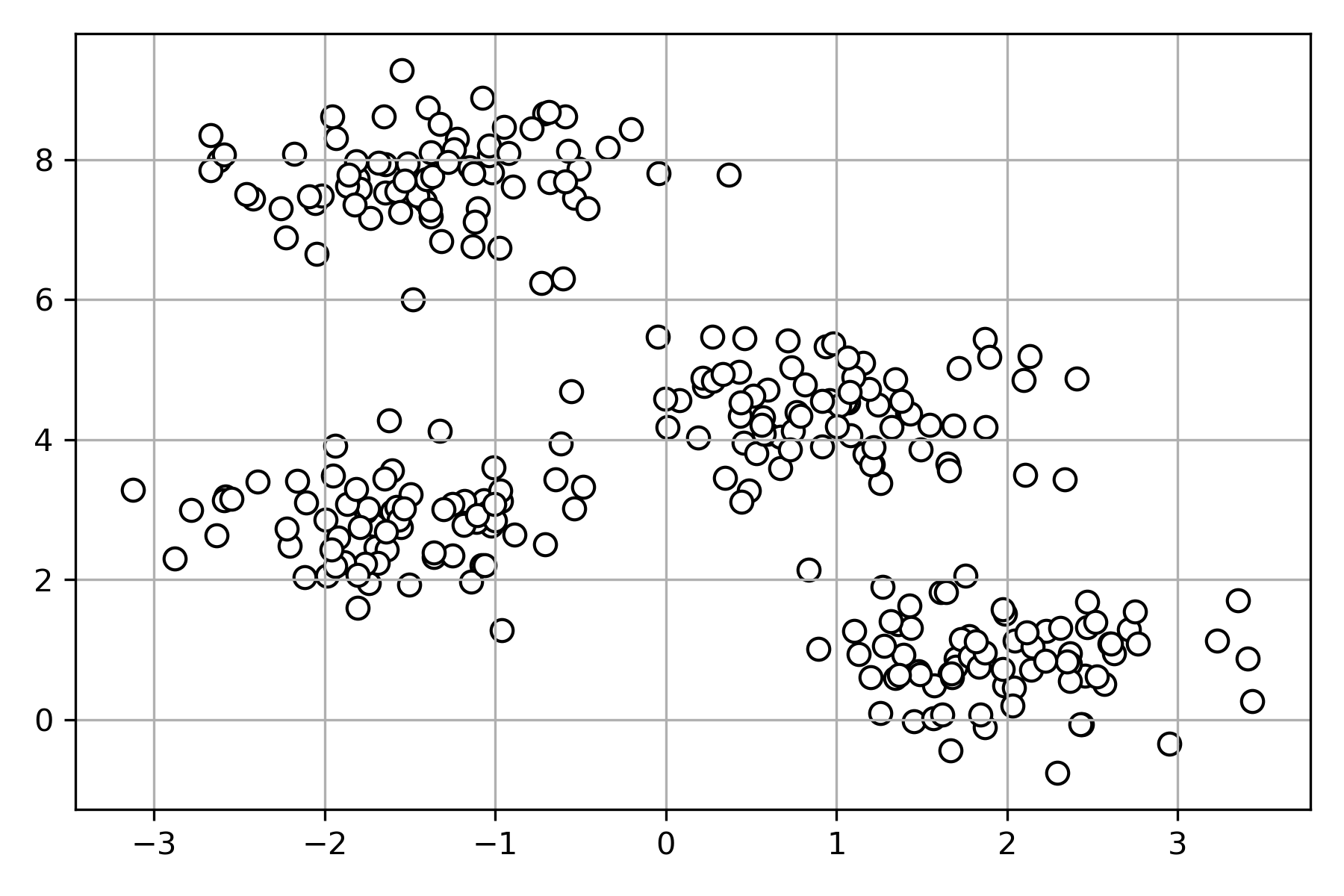
#ランダムにデータセットを作成。
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
X,y = make_blobs(n_samples=300,
                 centers=4,
                 cluster_std=0.6,
                 random_state=0)
plt.scatter (X[:,0], X[:,1], c='white', marker='o', edgecolor='black', s=50)
plt.grid()
plt.tight_layout()
plt.show()

#エルボー法を使い適したクラスタ数を求める。
from sklearn.cluster import KMeans
distortions = []
for i in range(1, 10):
    km = KMeans(n_clusters=i, 
                init='k-means++', 
                n_init=10, 
                max_iter=350, 
                random_state=0)
    y_km = km.fit_predict(X)
    km.fit(X)
    distortions.append(km.inertia_)
plt.plot(range(1, 10), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.tight_layout()
plt.show()

#シルエット法を使い適したクラスタ数を求める。
import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples

km = KMeans(n_clusters=4, 
            init='k-means++', 
            n_init=10, 
            max_iter=350,
            tol=1e-04,
            random_state=0)
y_km = km.fit_predict(X)

cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
    c_silhouette_vals = silhouette_vals[y_km == c]
    c_silhouette_vals.sort()
    y_ax_upper += len(c_silhouette_vals)
    color = cm.jet(float(i) / n_clusters)
    plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0, 
             edgecolor='none', color=color)

    yticks.append((y_ax_lower + y_ax_upper) / 2.)
    y_ax_lower += len(c_silhouette_vals)

silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="--")

plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.tight_layout()
plt.show()

シルエット係数の計算
silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
    c_silhouette_vals = silhouette_vals[y_km == c]
    c_silhouette_vals.sort()
    y_ax_upper += len(c_silhouette_vals)
    color = cm.jet(float(i) / n_clusters)
    plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0, 
             edgecolor='none', color=color)

    yticks.append((y_ax_lower + y_ax_upper) / 2.)
    y_ax_lower += len(c_silhouette_vals)

silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="--")    
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.tight_layout()
plt.show()

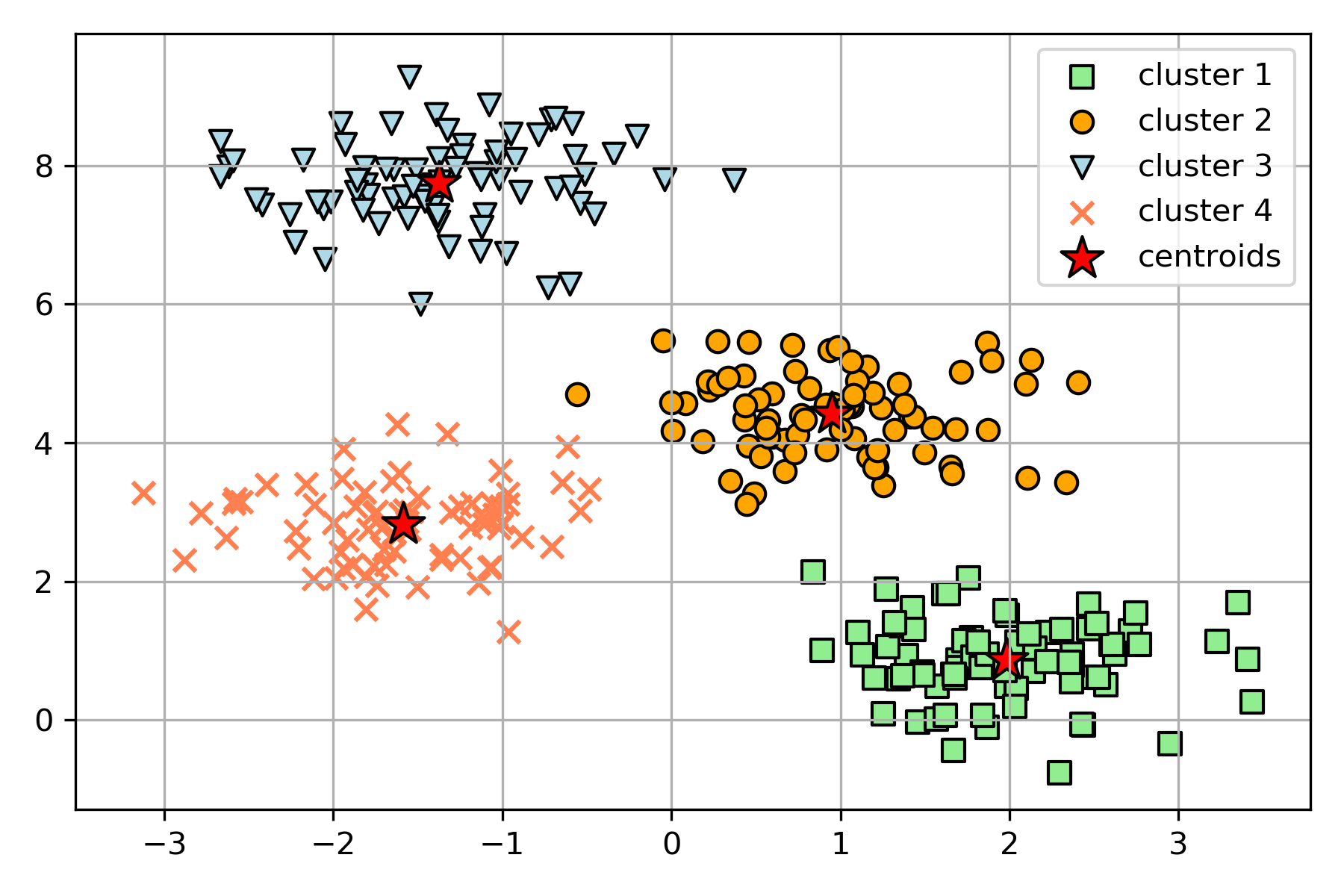
#k-means法によるクラスタリングのプロット
from sklearn.cluster import KMeans
km=KMeans(n_clusters=4,
          init='k-means++',      
          n_init=15,
          max_iter=350,
          tol=1e-04,
          random_state=0)
y_km=km.fit_predict(X)

plt.scatter(X[y_km==0,0],
            X[y_km==0,1],
            s=50,
            c='lightgreen',
            edgecolor='black',
            marker='s',
            label='cluster 1')
plt.scatter(X[y_km==1,0],
            X[y_km==1,1],
            s=50,
            c='orange',
            edgecolor='black',
            marker='o',
            label='cluster 2')
plt.scatter(X[y_km==2,0],
            X[y_km==2,1],
            s=50,
            c='lightblue',
            edgecolor='black',
            marker='v',
            label='cluster 3')
plt.scatter(X[y_km==3,0],
            X[y_km==3,1],
            s=50,
            c='coral',
            edgecolor='black',
            marker='x',
            label='cluster 4')
plt.scatter(km.cluster_centers_[:,0],
            km.cluster_centers_[:,1],
            s=200,
            marker='*',
            c='red',
            edgecolor='black',
            label='centroids')
plt.legend(scatterpoints=1)
plt.grid()
plt.tight_layout()
plt.show()

k-means法の欠点

1. 初期値に依存する。
2. 外れ値の影響を受けやすい。
3. 各データが1つのクラスタにしか所属できない。
4. クラスタの個数をあらかじめ決定しなければならない。（クラスタの個数に正解はない。）

さいごに

以上がk-means法についてである。今回は数学的要素を最小限に抑え、同手法がどのように成り立っているかに重きを置き紹介した。クラスタリングの中で最も有名と言っても過言ではないk-means法は、データサイエンスや機械学習をやる上で必ず目にするだろう。加えて、クラスタリングはWebマーケティングや画像処理等にも活用できるなど利用用途は幅広く知っておいて損はない手法だろう。

定期的にメルマガでも情報配信をしています。
ご希望の方は問い合わせページに「メルマガ登録希望」とご連絡ください。

参考文献

DATAFLAIR TEAM (2019) 『Data Science K-means Clustering: In-depth Tutorial with Example』Retrieved from LINK .

Hastie, Trevor et al. (2009)『The Elements of Statistical Learning: Data Mining, Inference, and Prediction Second Edition』. (杉山将　他　訳)

Pelleg, Dan and Moore, Andrew (2000) 『X-means: Extending k-means with efficient estimation of the number of clusters』. Morgan Kaufmann.

Raschka, Sebastian and Mirjalili, Vahid (2017)『Python 機械学習プログラミング』. (株式会社クイーブ　訳). インプレス.

VanderPlas, Jake (2016) 『Python Data Science Handbook: Essential Tools for Working with Data』.

平井有三（2012）『はじめてのパターン認識』. 森北出版株式会社.