1.判別分析の定義

判別分析とは、統計学上のデータ解析手法の一つである。
特定のグループに分かれているデータを元にどのような基準で判別されているか解析する。
そして、どちらのグループがA群に属され、B群に属されるかを予測する分析のことである。

2.判別分析の成り立ち

1936年にロナルドフィシャーによって線形判別分析が発表され、これを元に分析手法が発達した。

3.判別分析の例

1.医療診断　
・喫煙の有無により癌の発病を予測
・検査結果から病気の有無の判別
2.選挙予測
・世論調査による法案の通過の有無予測
・立候補政党から立候補者の当落の判別
3.受験合格の予想
・模擬試験の採点から志望校の合格を予測
・勉強時間等から合否の判別
4.マーケティングの予測
・企業の倒産の判別
・画像の色や形から異常の判別
・顧客の発注の有無判別

4.判別分析の種類

A 群とB群を線で仕切りA群に属するかBに属するかを分ける方法には、以下の2種類がある。
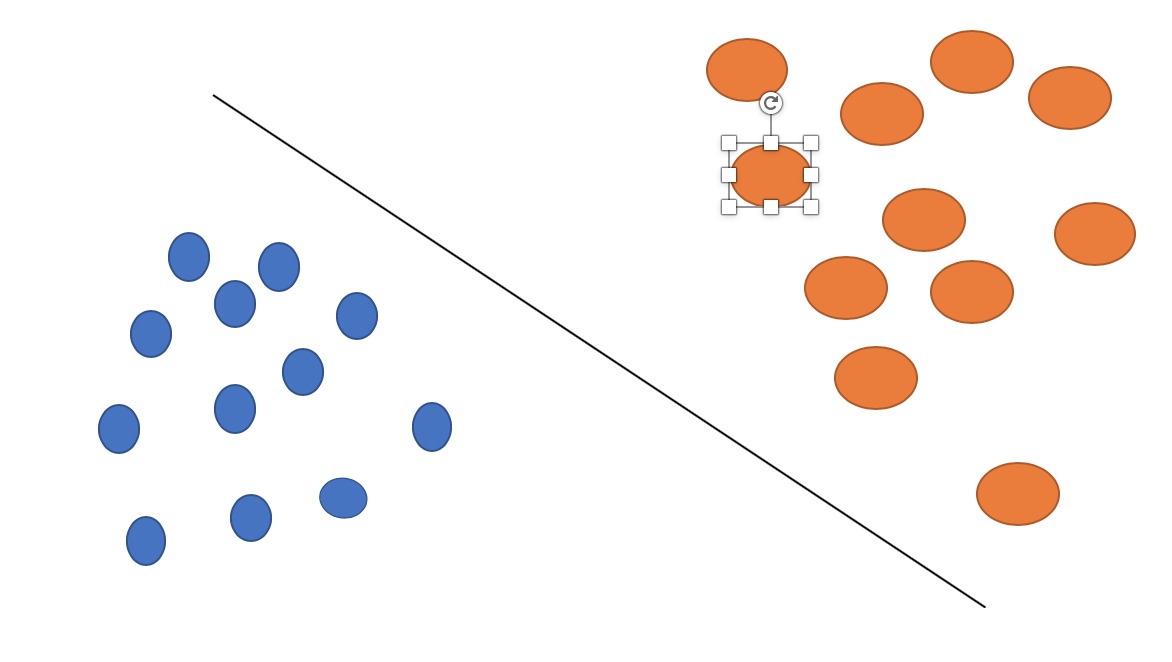
1.線形判別関数で仕切る
線形判別関数とは、2つのクラスを最もよく判別できる直線を求める手法の事である。

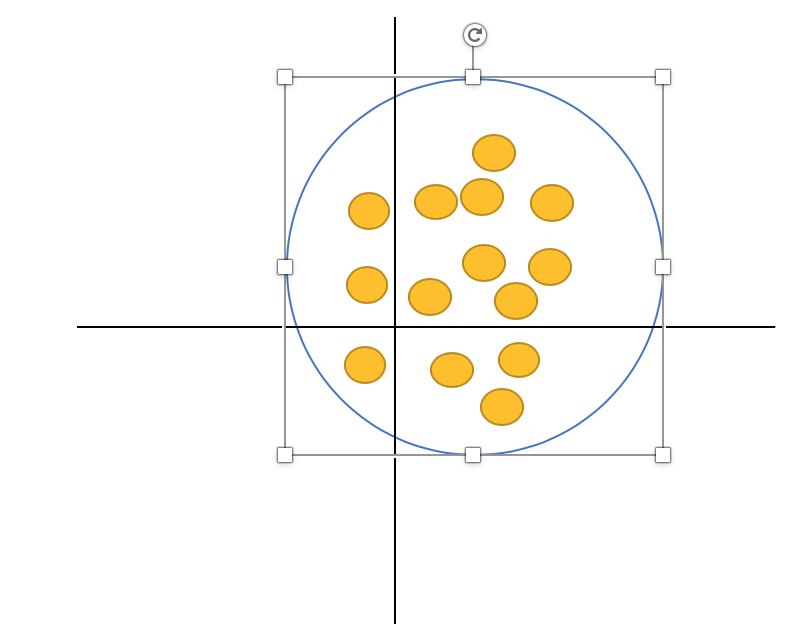
2.マハラノビス距離で仕切る
マハラノビス距離とは、データの分布の広がりを加味した距離のことで2点間の直線距離を 標準偏差で割った値を2乗して求められる距離のことである。

5.判別分析の手順

1.事例
例)A塾では、生徒をなるべくいい学校に合格させたい。
そこで生徒の能力で一番上の志望校をお勧めするために模試を作った。
２.分析の目的
模試によって生徒の志望校の合否判定を行うこと。
３.データ準備
今回の目的のために、様々なデータを集めた。
例)合格点数、志望者数、偏差値等のデータ
採用するデータを集める際には、人間が集めるためアナログな部分がある。
４.判別分析ツール
統計ソフトを使いそれらのデータを入れて計算する。
データは相関性の強いもののみを使用して、線形判別係数により判別式を作る。
５.分析結果の活用
判別式で出た数値を元に合否を判断する。
今回の場合、判別式でyが1以上であれば、合格になる可能性が高いと判断できる。 そして、A塾はこの模試の結果に基づいて生徒にもっとも良いと思われる学校をお勧めする。

6.まとめ

判別分析は、様々な場面で利用することができる。
しかし、データの選択をする際には、人間が選ぶため相関性が高いのか判別して式に落とし込む必要がある。